K-Means Clustering¶
Learning Objectives
Understand data clustering
Learn the k-mean algorithm
Write a test generator for creating test cases
Implement the algorithm in Python
Clustering Data¶
Consider the following scenario: A department store is planning the annual promotion. The store wants to give customers discount coupons based on their purchase history. If a customer has purchased a desk at this store, the customer is given a coupon for a desk. If a customer has purchased shoes, the customer is given a coupon for shoes. If a customer has purchased a jacket, the customer is given a coupon for a jacket. The store sells thousands of products and it does not want to give one type of coupon for each product because doing so would create thousands of types of coupons. It would be too expensive making so many types of coupons and programming the checkout machines to recognize these many types of coupons. Instead, the store wants to provide only a few (say 10) types of coupons. The store wants to group the customers based on what they bought together. For example
If a customer has bought shirts, shoes, and a sweater together, this customer is given a coupon for clothes.
If another customer has bought a desk, a dining table, and four chairs, this customer is given a coupon for furniture.
If a third customer has bought a tie and shoes, this customer also receives a coupon for clothes (not for furniture).
If the fourth customer has bought chair and a desk, this customer receives a coupon for furniture (not for clothes).
The problem is that the store does not know how to group the customers so that the same group of customers gets the same coupon. In other words, the store wants to divide the customers into groups so that the customers in each group have bought similar items. The discussion above assumes that customers would likely buy what they have already bought. In reality, stores would give customers coupons for what they may buy later. For example, if a customer has bought a desk, the customer is unlikely to buy another desk soon. Instead of giving a coupon for another desk, the store may give a coupon for buying a chair. If a customer has bought a jacket, the store may give a coupon for a sweater.
Consider another example: A research project wants to find the commonalities among lung cancer patients. They want to divide the patients into group based on personal information and behavior, such as age, location, occupation, education, marital status, diet, amounts of sleep, the food they eat, etc. They want to know whether one group has more patients than the other groups.
Both examples are clustering problems: these problems divide data (people in both cases) into groups so that the data inside each group is similar and the data in different group is dissimilar. This is unsupervised learning because there is no teacher telling computers whether two pieces of data belong to the same group. The correct answer depends on the other pieces of data.
Clustering into Groups¶
Consider the department store coupon problem again. Suppose the store decides to issue exactly ten types of coupons. The problem becomes dividing the customers into ten groups based on their purchase history. This section describes the k-mean clustering algorithm; here, \(k\) is a number assigned to the problem as the number of groups. For the department store, \(k\) is 10. Before explaining how this clustering method works, let us understand what this method wants to accomplish. An obvious question is how to decide the value of \(k\). This book will discuss that later.
Suppose there are \(n\) data points (each point is a person): \(x_1\), \(x_2\), …, \(x_n\). Each data point is a vector. The department store considers these products:
refrigerator
washer
dryer
jackets
shirts
shoes
pants
sweaters
For example, \(x_1 = <1, 0, 0, 3, 5, 0, 0, 2>\) means that in the past twelve months the first customer has bought one refrigerator, no washer, no dryer, three jackets, five shirts, no shoes, no pants, and two sweaters. If \(x_2 = <0, 1, 1, 0, 0, 1, 0, 0>\) means the second customer has bought no refrigerator, one washer, one dryer, no jackets, no shirts, one pair of shoes, no pants, and no sweater.
Define K-Mean Clustering Problem¶
We want to group these \(n\) data points into \(k\) clusters: \(C_1\), \(C_2\), …, \(C_k\). Obviously \(k\) must not exceed \(n\). In reality, \(k\) is usually much smaller than \(n\), i.e., \(k << n\). Each cluster contains a set of data points. In this book, a vector uses a lower case letter such as \(x\). A set uses an upper case letter such as \(C\). The following properties must be satisfied:
A data point must belong to one cluster: \(\forall i, 1 \le i \le n, \exists m, 1 \le m \le k\), such that \(x_i \in C_m\). This means for any value of \(i\) between 1 and \(n\) (inclusively), there is a value \(m\) between 1 and \(k\) (inclusively), such that \(x_i\) is an element of \(C_m\).
Each cluster contains one or more data points, i.e., \(|C_j| \ge 1\), for \(1 \le j \le k\). In other words, an empty cluster cannot be accepted.
The clusters together includes all data points: \(C_1 \cup C_2 \cup ... \cup C_k = \{x_1, x_2, ..., x_n\}\).
A data point must not belong to two or more clusters: \(\forall i, 1 \le i \le n\) if \(x_i \in C_j\) and \(x_i \in C_m\) then \(j = m\), here \(1 \le j, m \le k\). To put it in another way, \(C_j\) and \(C_m\) has no overlap if \(j \ne m\): \(C_j \cap C_m = \emptyset\).
How is the problem defined? Suppose \(D\) (as distance) defines how dissimilar the data points of each cluster. If the data points are quite similar, \(D\) is small. If the data points are quite dissimilar, \(D\) is large. The goal is to assign \(x_1\), \(x_2\), …, \(x_n\) to \(C_1\), \(C_2\), …, \(C_k\) so that
\(\min \underset{j = 1}{\overset{k}{\sum}} D(C_j)\)
is as small as possible.
This is a minimization problem. A minimization problem aims to make a quantity, called the cost function, as small as possible. Minimization problems are optimization problems, so are maximization problems. A maximization problem aims to make a quantity, called the profit function or score function, as large as possible.
How is \(D\) defined? It can be defined in many ways. One commonly used definition is the sum of pairwise Euclidean distance:
\(D(C_j) = \underset{x_r, x_s \in C_j}{\sum} (x_r - x_s)^ 2\)
If \(x_r\) and \(x_s\) are \(p\)-dimensional vectors: \(x_r = (x_{r1}, x_{r2}, ..., x_{rp})\) and \(x_s = (x_{s1}, x_{s2}, ..., x_{sp})\). The distance of them is defined as the sum of the square of the difference in each dimension:
\((x_r - x_s)^ 2 = \underset{i = 1}{\overset{p}{\sum}} (x_{ri} - x_{si})^2\).
It is common to divide \(D(C_j)\) by the number of data points in \(C_j\) so that clusters of different sizes are treated equally. Thus, \(D(C_j)\) is redefined as
\(D(C_j) = \frac{1}{|C_j|} \underset{x_r, x_s \in C_j}{\sum} (x_r - x_s)^ 2\).
Rewrite the cost function as
\(\min \underset{j = 1}{\overset{k}{\sum}} \frac{1}{|C_j|} \underset{x_r, x_s \in C_j}{\sum} (x_r - x_s)^ 2\).
Number of Solutions for Clustering¶
Deciding the proper value of \(k\) is a difficult problem because there are many possible solutions when \(n\) and \(k\) are large. How many possible solutions are there? This is equivalent to the set partition problem: divided a set of \(n\) elements into \(k\) non-overlapping non-empty subsets. Suppose the \(n\) data points can be assigned to any of the \(k\) clusters, there are \(k^n\) possibilities. This, however, allows empty clusters. Thus, we have to exclude the situation when one cluster is empty. In this case, there are \((k-1)^n\) options. If two clusters are empty, there are \((k-2)^n\) options. Continue until all except one cluster is empty. The total number of options is
\(k^n - (k-1)^n - (k -2) ^ n ... - 1^n = k^n - \underset{i = 1}{\overset{k-1} \sum} (k-i)^n\).
K-Mean Algorithm¶
When \(n\) and \(k\) are large, there are too many possible solutions and finding the best solution (or one of the best solutions, if several solutions are equally good and better than the other solutions) would be difficult. Instead of find the best solution, a heuristic, called the k-mean algorithm, usually finds good solutions. This is the step of the k-mean algorithm:

Figure 37 K-Mean Algorithm¶
A cluster’s centroid is the center of the data points assigned to this cluster. For cluster \(C_j\), its centroid is
\(\frac{1}{|C_j|} \underset{x_r \in C_j}{\sum} x_r\).
Please remember that each data point is a \(p\)-dimensional vector.
This is a heuristic solution, meaning that the solution often works but there is no assurance. The solution may fail in some cases. For many problems, finding the best solution (or solutions) can be computationally difficult because there are too many possibilities to check. Instead of finding the best solution, an algorithm is adopted to find “good enough” solutions fast. For the k-mean clustering problem, there is no easy way to determine the best value of \(k\). Thus, there is not clearly defined best solution.
Generate Test Cases¶
Before showing the implementation in Python, this section discusses how to generate test cases. Lacking test cases of known properties is one common problem in developing software for machine learning. The purpose of machine learning is to recognize unknown patterns in data. How can we know that the programs are correct if we do not know what the programs should find? Two methods are commonly used:
Creating simple test cases manually with known patterns.
Adopting widely used test cases whose patterns have already been studied.
The first methods is restricted to only very small test cases that are unlikely to have sophisticated patterns needed to test computer programs. The second methods, in contrast, may have sophisticated patterns but the data may be too complex for identifying problems in the programs.
Another approach is to write another program (or several programs) as a “test case generators” to generate the test cases of known patterns. More specifically, for this problem, we can write a program that generates \(n\) data points in \(k\) clusters (\(n > k\)). Since the data points are generated intentionally, it is easy to test whether the \(k\)-mean program is correct.
Writing a good test case generator takes some thinking because the
generator has to consider many different possible properties. The
programs in this chapter handles integers only because floating-point
numbers have limited precision and sometimes give surprising results,
to be discussed later in this book. This program generates two output
files: data.txt and cluster.txt. The first file has \(n\)
lines and each line has \(p\) integers. The second file also has
\(n\) lines; each line has the same \(p\) integers, following
by one integer between :math`0` and \(m - 1\) to indicate which
cluster this line belongs to.
#! /usr/bin/python3
# main.py for testgen.py
# Generate test cases for k-mean clustering program
import sys
import testgen
import argparse
def checkArgs(args = None):
parser = argparse.ArgumentParser(description='parse arguments')
parser.add_argument('-p', '--overlap', type = bool,
help = 'can clusters overlap', default = False)
parser.add_argument('-d', '--dimension', type = int, default = 2)
parser.add_argument('-c', '--cluster', type = int,
help = 'number of clusters', default = 3)
parser.add_argument('-m', '--minc', type = int,
help = 'minimum size of a cluster', default = 10)
parser.add_argument('-M', '--maxc', type = int,
help = 'maximum size of a cluster', default = 15)
parser.add_argument('-o', '--output',
help = 'output file name', default = 'data.txt')
parser.add_argument('-g', '--group',
help = 'cluster file name', default = 'cluster.txt')
args = parser.parse_args(args)
return args
if __name__ == "__main__":
args = checkArgs(sys.argv[1:])
testgen.testgen(args)
# testgen.py
'''This program randomly assigns the center of each cluster within
(-s, s) for each dimension. The clusters are distributed within (-sm,
sm). Then, the points of each cluster are within (-span, span) of the
center. If the points are truly random, span is as large 4s (allowing
the clusters to overlap). If overlaping is not allowed, span is only
s/3 (integer).
'''
import sys
import random
def testgen(args):
t = args.overlap
d = args.dimension
m = args.cluster
q = args.minc
r = args.maxc
output1 = args.output
output2 = args.group
# check whether the arguments are acceptable
if ((d < 1) or (m < 2) or (q < 3) or (r < q)):
sys.exit('invalid values for the arguments')
# print (args)
s = 1000 # size of each cluster
# print (t, d, m, q, r, s, output1, output2)
try:
fout1 = open(output1, 'w')
fout2 = open(output2, 'w')
except:
sys.exit('open fail')
# initialize the center of the first cluster
span = int(s / 3)
# centers are two-dimensional (m rows and d columns) arrays for
# the centers of clusters
centers = []
for cl in range (0, m):
newcenter = list(range(-m, m))
random.shuffle(newcenter)
# pick the first d elements and
# multiple every element by s
newcenter = [i * s * m for i in newcenter[0:d]]
centers.append(newcenter)
if (t == True):
span = 4 * s
cl = 1
for cl in range (0, m):
n = random.randint(q, r)
# how many point in this cluster
for dp in range (0, n):
# data point
line = ''
for dim in range (0, d):
# dimension
x = centers[cl][dim] + random.randint(-span, span)
line = line + str(x) + ' '
fout1.write(line + '\n')
fout2.write(line + ' ' + str(cl) + '\n')
fout1.close()
fout2.close()
TO DO: Need to explain the program
To run the program using the default values, type python3 main.py. This is an example output data.txt:
-50030 10279 -99947 39712 29919 -69795
-50181 10144 -100071 39734 30324 -69678
-49822 10148 -99714 40172 29897 -70056
-50165 10050 -99840 39780 29822 -69682
-50200 10187 -100147 40215 30200 -69992
-50238 9720 -99760 39966 29788 -69824
-50201 10030 -100081 39815 30253 -69881
-50237 9864 -100209 39795 30021 -70001
-50108 9874 -100212 39840 29914 -70272
-49975 10278 -99817 40243 29967 -70200
-50213 9948 -99943 40194 30037 -70114
-50294 9977 -99772 39786 30001 -69860
-49934 9947 -100331 39714 29680 -70067
-49704 9868 -100317 40035 30016 -69758
-49667 10304 -99885 40009 29673 -69838
-49975 9873 -99704 39796 30246 -69745
-49847 10279 -100253 39952 30151 -69976
-49993 10081 -100118 39713 29683 -69669
-50091 9680 -99981 39989 30054 -69890
-49723 9722 -99979 40126 29879 -70055
-49852 9681 -100074 40124 30048 -70165
-50115 9966 -100039 40332 30297 -70323
-49812 9951 -99884 40142 30040 -69919
-50138 10249 -100300 39750 30116 -69689
-49743 10079 -99995 39823 29739 -70056
-49677 9763 -99900 40032 29795 -69859
-49809 10001 -100207 39883 29781 -69760
-49924 10199 -99840 40166 29890 -70085
-50086 9789 -99808 39780 30044 -69900
-50014 9788 -100235 40131 30071 -69777
-49963 9690 -99850 39885 30274 -69736
-49929 10013 -99856 40194 30048 -70323
-50276 10165 -99800 39798 30204 -70297
-49810 10211 -99678 40228 30109 -70204
-50238 10137 -100234 40054 29898 -70078
-50254 10272 -99890 39926 29692 -69952
-50276 9765 -99972 39698 29912 -69845
-50268 9796 -100001 39763 29816 -69852
-50032 9895 -100168 40196 29949 -69965
-49884 9831 -100101 39835 30026 -70085
-50233 10304 -100161 39788 30033 -69900
-49959 10040 -99996 40299 29682 -69691
-50193 10015 -99950 39769 29870 -70174
-49772 9937 -100267 40095 29678 -69942
-49678 10147 -100182 40066 30309 -69879
-50193 10059 -99847 39726 30322 -69677
-49681 9977 -100031 39951 30154 -69979
-50198 9670 -100140 39724 29921 -69824
-49940 9725 -99738 39678 30271 -69880
-50263 9858 -100212 40011 29728 -70155
-50074 10129 -99976 39861 29955 -69960
-49957 10150 -100171 40279 30176 -70040
-50176 9805 -100160 40044 29852 -69962
-49962 10165 -99895 40152 30248 -69715
-49734 9719 -99990 39887 29966 -70208
-49757 9932 -100022 40065 29774 -69982
-49696 10260 -99830 40200 30078 -69878
10108 1 20113 -99800 50165 60174
9969 -178 20092 -99709 49798 59816
9714 -211 20276 -99999 50301 60239
10059 -94 20281 -100113 49997 59801
9709 74 19852 -99858 50053 59710
9669 -100 19847 -99945 49996 60122
10230 -305 20000 -99833 49993 59698
10175 -141 20137 -100035 49881 60170
10069 198 19781 -100242 49717 59789
10295 146 19863 -99965 49932 59786
9884 39 19951 -99741 50197 60147
10134 -279 20317 -100305 50005 59972
9908 -29 20244 -100202 49965 59745
9895 -167 19765 -100270 50097 60281
9961 65 20060 -100110 49831 60113
9771 213 20023 -100260 49980 60053
9798 -267 19839 -99793 49668 59952
9755 -237 20257 -99977 50057 60266
10216 -106 19995 -99826 49766 60085
9718 -195 19992 -100001 50213 60200
10174 -121 20162 -99926 49700 59738
10322 49 19962 -100195 49752 59789
10285 225 20191 -100200 50195 60140
10155 -227 20084 -99686 49878 59825
9830 -137 19912 -99670 49768 60091
9798 -112 19685 -100300 50207 60023
10236 212 20053 -100080 50195 59845
9779 166 20004 -99699 49996 59863
9940 -324 19828 -100263 50070 59998
10256 -181 19961 -99755 49670 59920
9838 -45 19884 -99920 49920 60179
9796 -85 20197 -99828 49781 59769
9689 107 20185 -100048 50219 59938
10188 3 20019 -100170 49760 59921
10076 -67 20087 -99891 50056 60201
10244 141 19882 -100274 50220 59911
10249 142 19999 -100019 50312 60248
10287 153 20173 -99905 50249 60269
10194 -189 19911 -99930 49942 59962
10302 -325 20116 -100150 50155 60014
9743 -277 20179 -100302 50190 59927
10319 -239 20224 -100304 49839 60127
10309 177 19815 -100149 50177 59998
10129 210 19811 -99769 50187 60249
10283 120 19736 -100105 49933 59956
9752 259 19670 -100002 50001 59827
10283 -90 19976 -100192 49894 59706
10062 204 19765 -99855 50080 60225
9819 -189 19858 -100109 50000 60173
10091 -149 20059 -99725 50051 60273
-60321 -49667 -19725 -39713 50292 80105
-60285 -49807 -20321 -39729 49713 80124
-59888 -49983 -20069 -39848 49857 80111
-60167 -50228 -19754 -40087 50234 79836
-60294 -50121 -20280 -39917 49986 80234
-59700 -49757 -20323 -40029 49870 80323
-59673 -49681 -20095 -39754 50017 79765
-59946 -50141 -20230 -39682 50295 79812
-59778 -50062 -19781 -39669 50191 79792
-60078 -49955 -20224 -40284 49922 80211
-60158 -50000 -20264 -39734 50073 79831
-60075 -49988 -20275 -40105 49936 79742
-59802 -49879 -19796 -39915 50143 80015
-60116 -50194 -20326 -40006 49747 79741
-60112 -50175 -19704 -39953 49908 79722
-60003 -49705 -20290 -39994 49786 80231
-60216 -49894 -20018 -40221 50026 80023
-60088 -49821 -20020 -40200 50142 80104
-60041 -50220 -19933 -40102 50174 79956
-59927 -50016 -20327 -40064 50315 79738
-60326 -49886 -20006 -40146 49991 80097
-59880 -50317 -19931 -40203 49741 79928
-60097 -49880 -19989 -39971 49926 80279
-60192 -49937 -20293 -39751 49896 80316
-60301 -49788 -20257 -40142 49947 80010
-59771 -50169 -20072 -39920 50165 79949
-59978 -50070 -19786 -39995 49965 79803
-60145 -49965 -19761 -40218 50070 79712
-60107 -50193 -19960 -39714 50259 79987
-60226 -49916 -20282 -40057 49856 79946
-60314 -50222 -19959 -39840 50251 80147
-60046 -49740 -19836 -39949 49983 79689
-60196 -49920 -20145 -40111 50036 79749
-59879 -50229 -20106 -39754 49810 80193
-60076 -50194 -20155 -40164 50248 79776
-59906 -49687 -20209 -40297 50079 80165
-59834 -49844 -19908 -40070 50080 79790
-60193 -50239 -20202 -40277 50101 79805
-59688 -50293 -19680 -39981 49943 79793
-59712 -50025 -20166 -39741 50228 80158
-60118 -50296 -19995 -40147 49766 80245
-60305 -50109 -19924 -39826 50164 79998
-59685 -50298 -20185 -40290 50064 80031
-60058 -49770 -19797 -39723 50264 79905
-60086 -50270 -20295 -39966 49952 79811
-60242 -50297 -19864 -39912 50026 79763
-60182 -49847 -19852 -40248 50300 80219
-60323 -49975 -19938 -40022 50089 80030
-59887 -50264 -20021 -39942 49989 80128
-60013 -50009 -19712 -40078 50279 79970
-60230 -50189 -20161 -39877 49789 80258
-59801 -49752 -19762 -40106 49939 80137
-60060 -49939 -19840 -39667 49798 80047
-59824 -50003 -20212 -39829 50087 79837
20298 -223 50131 -20258 40261 60312
19952 319 50188 -19668 40065 59729
20173 101 49884 -19691 40265 59765
20151 -139 50047 -20042 39961 59767
20022 277 50019 -20188 39760 60234
20190 -99 50259 -20245 39733 59760
19878 -110 50054 -20268 39999 60062
19957 132 50115 -20236 40017 60040
19947 -72 49878 -19977 39965 59765
20277 96 50130 -19689 39928 60317
19864 44 49724 -20230 39761 60208
20184 14 49809 -19780 39782 59962
19703 66 50096 -20272 39896 59803
20092 -224 50160 -20136 40152 60172
20208 -151 49872 -19777 39904 60283
19992 292 49900 -20181 40083 59919
19738 228 50223 -20255 39803 59736
19983 108 49796 -19799 40260 60131
20284 207 50174 -19752 40099 60261
20061 -74 49859 -20269 40313 59710
19827 51 50215 -19946 39801 60060
19986 -102 49963 -20078 40184 59880
20069 295 50254 -19976 40251 60314
20292 35 49853 -19847 40329 60322
20122 196 49772 -19668 39840 60287
20211 253 50088 -19901 40147 59674
20331 -86 50085 -19875 39879 60208
19830 251 49949 -19839 40011 60333
19745 149 50176 -19901 40033 60155
19732 -179 49743 -20292 40240 59986
19774 317 49862 -20230 39791 59718
19802 287 49877 -20158 40307 60306
19889 171 50032 -19890 40035 59773
19991 229 49744 -20088 39875 60050
20164 84 50167 -20174 40062 60168
20215 -255 49769 -20180 40109 60143
19890 -10 49821 -20311 40066 59909
19829 44 50200 -20172 39988 59967
19865 -298 50139 -19956 39957 60156
19810 -29 49907 -20020 40104 60279
20244 281 50275 -20000 39735 59930
20141 -198 50089 -20232 40006 59672
19827 115 50097 -19787 39955 60230
19686 319 49906 -19869 40018 60248
20068 97 49913 -20079 40084 60292
20018 319 50234 -20174 39886 60254
19686 71 49813 -19681 39907 59827
20301 114 49682 -20044 40326 59737
20272 65 50294 -19862 40260 60016
20243 -331 49776 -20238 40209 59948
19789 187 49989 -20238 39926 59965
19715 101 50134 -19738 39704 60254
19708 -258 49973 -20012 40287 59985
20303 -185 49861 -20081 40211 59866
-59787 -69961 -29943 40058 -20135 -99983
-59828 -70177 -29965 40272 -19770 -100169
-59933 -69745 -29778 40209 -20262 -99700
-59713 -69682 -30141 40216 -19872 -99774
-60043 -70023 -29984 40191 -20269 -99725
-59992 -70271 -30222 40079 -20054 -99994
-59836 -70273 -30022 40328 -20196 -100294
-60322 -69992 -29680 39918 -20155 -100114
-60002 -70015 -30323 40230 -20156 -100127
-60194 -69760 -30329 39906 -20288 -100278
-59832 -70148 -29699 39719 -20003 -100252
-59732 -69871 -30125 39783 -20045 -100071
-59868 -70007 -29917 40326 -20118 -100139
-60325 -70290 -29807 39910 -20184 -100259
-60233 -70116 -29843 40000 -20173 -99952
-59904 -70288 -29680 40321 -20154 -99829
-60029 -70056 -29689 39898 -20002 -99989
-60268 -69992 -29699 40143 -19937 -99683
-59744 -70179 -29877 40022 -20272 -99773
-60201 -69817 -30184 40299 -20226 -99779
-59800 -69812 -29939 39973 -19910 -99803
-59898 -70159 -30263 40112 -20139 -99672
-60041 -69853 -30329 40315 -19861 -100050
-59898 -70244 -29798 39727 -19907 -99952
-59815 -70027 -29850 40250 -19948 -100307
-59722 -70244 -30124 39710 -19901 -100210
-59928 -70137 -29833 40027 -19992 -100210
-59742 -69926 -30293 39945 -20071 -99869
-59729 -69836 -30042 39690 -19854 -99709
-60040 -69689 -29788 39929 -20036 -100328
-59702 -69909 -29978 40144 -19683 -100266
-60183 -70244 -29842 39696 -19832 -100141
-60122 -69895 -30119 39884 -20172 -100040
-59722 -69977 -30015 40013 -20080 -100013
-60296 -70277 -30111 40306 -19867 -99807
-59736 -70266 -29998 39740 -19730 -99842
-59988 -70316 -30071 40296 -20087 -100151
-59758 -69832 -30048 39812 -19920 -100298
-60305 -69842 -29976 39834 -20206 -100120
-60096 -70234 -29684 40272 -20218 -99812
-60255 -70194 -29901 40032 -19962 -100170
-59847 -69933 -30319 39971 -20103 -100232
-59860 -69772 -29964 39677 -20292 -100183
-60283 -69762 -29965 39804 -19736 -99803
-60017 -69837 -29921 39932 -19748 -100323
-59982 -70006 -30242 40305 -19836 -100332
-59976 -69884 -29684 40129 -19814 -100132
-59923 -70096 -29688 39909 -19737 -100324
-59833 -69826 -30050 40194 -19746 -99891
-60148 -69686 -29944 40197 -20132 -100050
-60025 -69847 -29998 40030 -20079 -99931
60178 -59956 -20289 -9680 10136 208
59785 -60315 -20208 -10216 10188 -269
59694 -60095 -19949 -9967 9997 164
59787 -59724 -19918 -9692 10018 -136
59998 -60251 -19888 -10178 9951 -255
60168 -59908 -19854 -10127 10021 -89
60077 -59956 -20218 -10006 9890 -66
59956 -59789 -20171 -9859 10049 -28
59687 -60296 -19699 -10029 10046 -99
59835 -59689 -20000 -9821 9741 253
59679 -59897 -19707 -10235 10133 185
60176 -59670 -20118 -10096 9747 330
60259 -60159 -19969 -9671 10228 303
60229 -60333 -20182 -9735 9736 169
59982 -60235 -20309 -9990 9667 -310
60216 -60206 -19735 -10314 9768 241
59953 -60120 -19689 -9942 10200 175
60265 -60214 -19967 -10078 9916 47
60180 -60219 -19886 -9951 9669 -286
59860 -59819 -20251 -9731 10182 106
60288 -60323 -19993 -10212 10140 249
59788 -59985 -19787 -9674 10180 324
60054 -60093 -19916 -10026 10264 -24
60037 -59874 -19899 -9718 10214 203
59975 -59780 -20304 -10209 10161 -158
60002 -60110 -19773 -10332 9723 38
60263 -59812 -20036 -9791 10018 19
60190 -60189 -19867 -9667 10132 -181
59807 -60244 -20255 -10156 10330 98
59777 -59888 -20260 -10104 9820 171
60323 -59985 -20181 -10186 9934 177
59969 -59690 -20329 -10160 9695 -309
59853 -59859 -19836 -10157 9777 288
60110 -60331 -19794 -10066 10046 -187
60045 -59836 -20323 -10147 9905 256
59951 -59831 -19667 -9836 10188 -62
60298 -60111 -19860 -10216 9931 293
60245 -59921 -20158 -9905 9791 298
59954 -60286 -20278 -9671 10186 -71
60306 -60333 -19899 -9995 9872 86
60147 -60073 -19852 -10147 9786 -143
60297 -59940 -19811 -9715 10061 79
60110 -60015 -20210 -10279 9857 240
60204 -59918 -19686 -9680 10104 -171
59890 -59926 -19771 -10075 9754 148
60250 -59892 -20012 -9701 9886 42
60268 -60262 -19873 -9753 9750 330
59872 -59782 -19832 -9872 9972 -209
59816 -59709 -19830 -10023 10089 -124
60257 -59831 -20228 -10049 10184 291
60286 -59995 -19893 -9923 9845 332
60247 -59694 -20111 -10184 9945 329
60007 -59700 -20284 -9819 10157 172
60236 -60274 -20020 -9893 10002 228
59997 -60287 -19683 -9914 9828 257
59788 -59825 -19847 -10296 10123 317
29939 -100196 89831 59698 -80311 49889
29953 -99775 89710 60246 -79692 50001
30107 -100254 90099 59876 -80167 50137
29702 -100166 89941 59901 -80333 50072
29821 -99756 89802 60261 -79954 49882
30054 -100216 90110 60232 -80016 50272
29854 -100155 89801 59964 -79668 50188
30132 -99969 89987 60263 -79698 50284
29829 -99765 89806 60169 -79698 50218
30097 -99920 89697 59847 -79757 49868
29709 -99921 89697 59720 -79779 49846
30019 -99745 89719 60257 -79737 49995
29996 -99950 90240 59747 -79894 49788
29967 -99809 90016 60008 -79859 49784
30197 -100238 89839 59815 -79886 49935
30327 -99690 89685 59769 -79696 50267
29725 -99805 89833 59694 -79995 49731
30294 -99731 90246 60193 -79706 49680
30164 -99919 89729 60331 -79975 49770
30138 -99962 90161 59741 -79684 50052
30070 -99745 90161 59884 -79895 50193
29795 -100011 89673 59863 -79835 50009
29732 -100213 90032 59697 -80184 49798
29911 -100182 90199 60113 -79976 50017
30079 -100110 90189 59909 -79710 50310
30317 -99681 90174 60194 -79970 49805
29891 -99949 90267 60282 -80167 49671
29999 -100032 90067 59817 -80181 49765
30065 -99740 90045 60069 -79769 50330
29897 -100125 89676 59894 -79688 50045
29823 -99688 90028 60286 -80327 50119
30225 -99958 89910 59989 -80207 49683
30143 -99714 90259 60187 -80188 50031
29825 -99933 89769 60230 -79711 50066
29974 -100255 90206 60137 -79692 50243
30240 -99778 89931 60111 -79962 49848
30127 -100205 89877 59937 -80201 49933
29794 -100075 90315 60047 -79825 50053
30004 -99671 90065 59761 -79757 50204
30187 -99700 89808 60290 -80169 50097
30126 -99836 89947 59712 -79779 50224
29864 -100207 89750 59959 -79730 49844
30065 -99762 89693 59688 -79911 49944
30089 -99859 90183 60158 -80101 49812
30031 -100332 90243 60215 -79976 49785
30011 -99961 90075 60181 -79818 49734
30060 -99688 89817 60103 -79748 49914
29863 -99901 89744 60283 -80096 50296
30116 -100285 89952 59996 -79844 50017
30271 -100060 90107 60017 -79745 49894
29691 -100189 90013 60169 -79918 49755
29750 -100231 90200 60008 -80132 50024
29936 -100123 89790 60242 -79885 49856
30025 -100011 90215 60036 -80069 49695
29903 -99825 90030 60145 -79926 50249
29885 -99764 89764 60218 -79988 50147
29939 -99694 89671 59810 -79836 50297
29894 -100020 89705 59746 -79958 50333
49809 -103 10169 19756 -39995 -10155
49750 80 9787 19885 -39801 -10312
49668 231 9914 19904 -40247 -10034
50036 -234 9697 20213 -40208 -9673
49920 -33 10224 20226 -40140 -10065
50168 -24 10143 20171 -39889 -10114
49862 269 9668 19726 -40268 -10114
50242 -235 9668 19691 -40147 -10322
50254 247 10054 19668 -39905 -9913
49725 179 9734 20060 -39996 -9896
50163 90 9770 20311 -39950 -9899
50064 205 9840 20023 -40210 -10242
49953 286 9974 20175 -39948 -9691
50169 55 10310 20206 -39790 -9919
50272 -241 9900 19714 -40061 -10325
50055 195 9787 19807 -39983 -9728
50028 71 9712 19700 -39811 -9832
49785 -146 10050 19914 -40316 -10203
50202 38 9778 20258 -40248 -9710
50080 -175 9772 19850 -40329 -10091
49927 190 10233 19866 -39918 -9908
49812 -5 10180 19745 -40280 -10030
50149 307 9983 19874 -39696 -9864
49826 124 9969 20234 -39745 -10188
50333 307 10245 20100 -39842 -9905
49823 -297 10240 20175 -39903 -9835
50113 299 9751 20321 -40086 -10326
50012 -228 9897 20010 -39970 -10261
49941 -170 9847 20133 -39964 -9900
49844 139 10279 19852 -40083 -9864
50279 93 9885 20071 -40187 -10052
49911 -200 10144 20245 -39882 -10318
49823 245 9676 20045 -39764 -10020
50118 -158 10254 20128 -40098 -10124
49754 111 10048 19860 -40162 -9983
50075 -64 10306 19865 -39977 -9809
49944 -109 10213 19762 -39727 -9761
50005 -185 9939 19745 -40300 -9840
49936 280 9913 20242 -40008 -9910
49986 294 10331 20093 -39880 -10150
49674 213 10177 19992 -39911 -10120
50280 -333 10129 20038 -40283 -10303
49840 89 10035 19966 -40061 -10100
50319 79 10260 20278 -39674 -9805
50132 -317 9985 19708 -39671 -10027
50149 328 10154 19726 -39859 -10318
50113 -158 9931 20081 -39723 -9835
50206 -48 9933 20238 -40029 -9974
50121 24 10235 20073 -39989 -9726
50198 -254 10228 19775 -39844 -10063
49697 -24 9751 20145 -40099 -10163
50313 -124 9674 20309 -39918 -10134
50226 -143 9841 19890 -40002 -9802
50199 -74 10310 20179 -39768 -10109
49757 213 10074 20293 -39763 -9845
50325 -244 9956 19716 -39766 -9857
49805 -21 10212 20189 -39692 -9726
49743 285 10213 19938 -40163 -9922
50041 -269 10303 19734 -40056 -9953
-20311 -333 -10225 -100005 29937 -50325
-19764 323 -9955 -100128 29744 -49743
-20033 241 -10206 -99731 29686 -49754
-20026 26 -9785 -100030 30252 -49883
-20051 -200 -9769 -100312 29835 -50103
-19711 -31 -9926 -100196 29846 -49867
-20311 230 -10017 -99978 29867 -49986
-19939 -270 -9739 -99733 30099 -49862
-19866 -196 -9969 -99978 30273 -49924
-20088 -35 -9867 -100314 30011 -49863
-19752 46 -10222 -100280 30013 -50320
-19752 68 -10236 -100195 30140 -49957
-19851 182 -9865 -99879 29909 -49968
-20312 -104 -10171 -100214 29719 -49748
-19889 92 -10238 -99987 30302 -49819
-20282 298 -10227 -99920 30240 -50223
-19768 -127 -9844 -100276 30139 -49780
-19813 -76 -9765 -100122 30294 -49685
-20196 196 -10137 -99989 30329 -49675
-19787 58 -10315 -99712 29702 -50153
-20006 -61 -10125 -99830 30209 -50035
-19780 -195 -9864 -100072 30081 -49977
-20081 -234 -9875 -100127 29969 -49760
-19943 -247 -9776 -100314 30113 -49670
-20324 174 -9759 -100091 29936 -50292
-20061 -41 -9984 -100205 30070 -49895
-19861 -71 -10073 -99938 30115 -50151
-19901 300 -9979 -99705 29899 -49784
-20005 218 -9738 -99963 29761 -50071
-20074 208 -9814 -99945 30272 -49670
-19819 165 -9955 -100005 29831 -49780
-20072 102 -9976 -99869 30060 -49968
-19760 -153 -9823 -99963 29707 -49969
-19894 -275 -10237 -100065 30269 -50015
-19823 -32 -10149 -100046 29804 -49828
-19720 170 -9782 -100088 30064 -50192
-20043 24 -10176 -100223 29721 -50309
-20160 235 -10101 -100301 30231 -50270
-20232 166 -9880 -100036 30160 -50019
-20166 228 -9761 -99678 29685 -49740
-19749 -153 -9831 -100055 29826 -50251
-19901 315 -10327 -99942 29858 -50304
-20157 312 -9704 -99759 29909 -49686
-20332 -117 -9798 -99705 30115 -50105
-19874 155 -10281 -99899 29953 -49827
-19678 -227 -10061 -100032 30309 -50332
-20044 38 -10150 -99746 30319 -49755
-20017 -9 -9692 -100326 30282 -50087
-20320 317 -9905 -100110 29837 -50055
-20293 -129 -10108 -99739 29798 -50124
-20078 -272 -10042 -99743 30072 -49869
-19672 92 -10030 -99961 30065 -50322
-60210 -50084 50223 59726 30222 -96
-60041 -50222 50027 59955 30250 -251
-60323 -50109 49824 60111 29908 274
-59908 -49792 49738 60155 29819 249
-60083 -50322 50010 60293 29921 -250
-60039 -49996 50193 60294 30325 59
-59936 -50323 49748 60112 30078 -225
-59837 -49779 49794 60141 29893 283
-59774 -49923 49754 59928 30306 -106
-60035 -50060 49952 60267 30290 105
-59790 -49934 49963 59993 30301 -219
-59896 -49969 50011 59709 29889 -133
-59955 -49839 49980 60269 30029 -141
-59981 -50297 49706 59949 29712 -40
-60018 -50297 50159 60211 30150 301
-60276 -49746 49767 60098 30250 20
-60191 -49993 49775 59829 30209 -240
-60067 -49680 50181 60077 30087 307
-59930 -50179 49879 59984 29890 -182
-59765 -50066 49749 60179 30190 -140
-59956 -50317 50252 59827 29683 137
-59862 -50207 50121 59920 29849 -243
-59738 -49718 49979 59931 30109 -213
-60299 -50145 50050 59866 29794 22
-59939 -50168 50221 60115 29788 270
-60115 -50182 49784 60079 29877 -166
-59819 -49990 50226 59709 30282 -30
-59854 -49807 50206 60173 30013 131
-60064 -49740 50123 60010 29827 -165
-59894 -49686 50283 60251 30127 192
-60013 -50205 49857 60129 29909 -18
-59896 -50002 49704 60054 29865 -165
-60007 -50141 49728 59885 29828 -229
-60085 -50298 50313 59811 29815 167
-60037 -50259 49864 60047 29985 -321
-59745 -50184 50231 59762 29753 170
-60201 -49715 50141 60283 29769 -237
-59859 -50241 49883 60169 30061 293
-60092 -49709 49912 59875 29700 182
-59943 -50228 49745 59860 30037 -121
-60098 -49843 50005 60104 29999 -178
-59705 -50121 49757 59721 30072 246
-60306 -49728 49963 60098 29969 -332
-60045 -50313 49712 59754 30246 293
-59814 -49858 49960 60125 29790 203
-60101 -49708 49718 59909 29687 124
-59861 -50280 49869 59952 29709 77
-60169 -50054 49719 59960 30333 -271
-59851 -49947 49882 60110 29706 -209
-59996 -50174 49751 60298 29893 66
-59892 -50062 49919 60076 30147 -304
-60198 -50054 49918 59900 30125 127
-60191 -49675 49849 60299 30067 -31
-60048 -49735 49990 59858 30141 5
-60164 -50213 49856 60080 29839 -47
-59776 -49747 50327 60296 30037 96
-59799 -49884 49688 60265 30208 -322
-59882 -50055 50231 59725 29863 -242
-59803 -49970 49691 59874 30102 -119
-60321 -50313 50219 60211 30120 -318
This is the corresponding cluster.txt.
-50030 10279 -99947 39712 29919 -69795 0
-50181 10144 -100071 39734 30324 -69678 0
-49822 10148 -99714 40172 29897 -70056 0
-50165 10050 -99840 39780 29822 -69682 0
-50200 10187 -100147 40215 30200 -69992 0
-50238 9720 -99760 39966 29788 -69824 0
-50201 10030 -100081 39815 30253 -69881 0
-50237 9864 -100209 39795 30021 -70001 0
-50108 9874 -100212 39840 29914 -70272 0
-49975 10278 -99817 40243 29967 -70200 0
-50213 9948 -99943 40194 30037 -70114 0
-50294 9977 -99772 39786 30001 -69860 0
-49934 9947 -100331 39714 29680 -70067 0
-49704 9868 -100317 40035 30016 -69758 0
-49667 10304 -99885 40009 29673 -69838 0
-49975 9873 -99704 39796 30246 -69745 0
-49847 10279 -100253 39952 30151 -69976 0
-49993 10081 -100118 39713 29683 -69669 0
-50091 9680 -99981 39989 30054 -69890 0
-49723 9722 -99979 40126 29879 -70055 0
-49852 9681 -100074 40124 30048 -70165 0
-50115 9966 -100039 40332 30297 -70323 0
-49812 9951 -99884 40142 30040 -69919 0
-50138 10249 -100300 39750 30116 -69689 0
-49743 10079 -99995 39823 29739 -70056 0
-49677 9763 -99900 40032 29795 -69859 0
-49809 10001 -100207 39883 29781 -69760 0
-49924 10199 -99840 40166 29890 -70085 0
-50086 9789 -99808 39780 30044 -69900 0
-50014 9788 -100235 40131 30071 -69777 0
-49963 9690 -99850 39885 30274 -69736 0
-49929 10013 -99856 40194 30048 -70323 0
-50276 10165 -99800 39798 30204 -70297 0
-49810 10211 -99678 40228 30109 -70204 0
-50238 10137 -100234 40054 29898 -70078 0
-50254 10272 -99890 39926 29692 -69952 0
-50276 9765 -99972 39698 29912 -69845 0
-50268 9796 -100001 39763 29816 -69852 0
-50032 9895 -100168 40196 29949 -69965 0
-49884 9831 -100101 39835 30026 -70085 0
-50233 10304 -100161 39788 30033 -69900 0
-49959 10040 -99996 40299 29682 -69691 0
-50193 10015 -99950 39769 29870 -70174 0
-49772 9937 -100267 40095 29678 -69942 0
-49678 10147 -100182 40066 30309 -69879 0
-50193 10059 -99847 39726 30322 -69677 0
-49681 9977 -100031 39951 30154 -69979 0
-50198 9670 -100140 39724 29921 -69824 0
-49940 9725 -99738 39678 30271 -69880 0
-50263 9858 -100212 40011 29728 -70155 0
-50074 10129 -99976 39861 29955 -69960 0
-49957 10150 -100171 40279 30176 -70040 0
-50176 9805 -100160 40044 29852 -69962 0
-49962 10165 -99895 40152 30248 -69715 0
-49734 9719 -99990 39887 29966 -70208 0
-49757 9932 -100022 40065 29774 -69982 0
-49696 10260 -99830 40200 30078 -69878 0
10108 1 20113 -99800 50165 60174 1
9969 -178 20092 -99709 49798 59816 1
9714 -211 20276 -99999 50301 60239 1
10059 -94 20281 -100113 49997 59801 1
9709 74 19852 -99858 50053 59710 1
9669 -100 19847 -99945 49996 60122 1
10230 -305 20000 -99833 49993 59698 1
10175 -141 20137 -100035 49881 60170 1
10069 198 19781 -100242 49717 59789 1
10295 146 19863 -99965 49932 59786 1
9884 39 19951 -99741 50197 60147 1
10134 -279 20317 -100305 50005 59972 1
9908 -29 20244 -100202 49965 59745 1
9895 -167 19765 -100270 50097 60281 1
9961 65 20060 -100110 49831 60113 1
9771 213 20023 -100260 49980 60053 1
9798 -267 19839 -99793 49668 59952 1
9755 -237 20257 -99977 50057 60266 1
10216 -106 19995 -99826 49766 60085 1
9718 -195 19992 -100001 50213 60200 1
10174 -121 20162 -99926 49700 59738 1
10322 49 19962 -100195 49752 59789 1
10285 225 20191 -100200 50195 60140 1
10155 -227 20084 -99686 49878 59825 1
9830 -137 19912 -99670 49768 60091 1
9798 -112 19685 -100300 50207 60023 1
10236 212 20053 -100080 50195 59845 1
9779 166 20004 -99699 49996 59863 1
9940 -324 19828 -100263 50070 59998 1
10256 -181 19961 -99755 49670 59920 1
9838 -45 19884 -99920 49920 60179 1
9796 -85 20197 -99828 49781 59769 1
9689 107 20185 -100048 50219 59938 1
10188 3 20019 -100170 49760 59921 1
10076 -67 20087 -99891 50056 60201 1
10244 141 19882 -100274 50220 59911 1
10249 142 19999 -100019 50312 60248 1
10287 153 20173 -99905 50249 60269 1
10194 -189 19911 -99930 49942 59962 1
10302 -325 20116 -100150 50155 60014 1
9743 -277 20179 -100302 50190 59927 1
10319 -239 20224 -100304 49839 60127 1
10309 177 19815 -100149 50177 59998 1
10129 210 19811 -99769 50187 60249 1
10283 120 19736 -100105 49933 59956 1
9752 259 19670 -100002 50001 59827 1
10283 -90 19976 -100192 49894 59706 1
10062 204 19765 -99855 50080 60225 1
9819 -189 19858 -100109 50000 60173 1
10091 -149 20059 -99725 50051 60273 1
-60321 -49667 -19725 -39713 50292 80105 2
-60285 -49807 -20321 -39729 49713 80124 2
-59888 -49983 -20069 -39848 49857 80111 2
-60167 -50228 -19754 -40087 50234 79836 2
-60294 -50121 -20280 -39917 49986 80234 2
-59700 -49757 -20323 -40029 49870 80323 2
-59673 -49681 -20095 -39754 50017 79765 2
-59946 -50141 -20230 -39682 50295 79812 2
-59778 -50062 -19781 -39669 50191 79792 2
-60078 -49955 -20224 -40284 49922 80211 2
-60158 -50000 -20264 -39734 50073 79831 2
-60075 -49988 -20275 -40105 49936 79742 2
-59802 -49879 -19796 -39915 50143 80015 2
-60116 -50194 -20326 -40006 49747 79741 2
-60112 -50175 -19704 -39953 49908 79722 2
-60003 -49705 -20290 -39994 49786 80231 2
-60216 -49894 -20018 -40221 50026 80023 2
-60088 -49821 -20020 -40200 50142 80104 2
-60041 -50220 -19933 -40102 50174 79956 2
-59927 -50016 -20327 -40064 50315 79738 2
-60326 -49886 -20006 -40146 49991 80097 2
-59880 -50317 -19931 -40203 49741 79928 2
-60097 -49880 -19989 -39971 49926 80279 2
-60192 -49937 -20293 -39751 49896 80316 2
-60301 -49788 -20257 -40142 49947 80010 2
-59771 -50169 -20072 -39920 50165 79949 2
-59978 -50070 -19786 -39995 49965 79803 2
-60145 -49965 -19761 -40218 50070 79712 2
-60107 -50193 -19960 -39714 50259 79987 2
-60226 -49916 -20282 -40057 49856 79946 2
-60314 -50222 -19959 -39840 50251 80147 2
-60046 -49740 -19836 -39949 49983 79689 2
-60196 -49920 -20145 -40111 50036 79749 2
-59879 -50229 -20106 -39754 49810 80193 2
-60076 -50194 -20155 -40164 50248 79776 2
-59906 -49687 -20209 -40297 50079 80165 2
-59834 -49844 -19908 -40070 50080 79790 2
-60193 -50239 -20202 -40277 50101 79805 2
-59688 -50293 -19680 -39981 49943 79793 2
-59712 -50025 -20166 -39741 50228 80158 2
-60118 -50296 -19995 -40147 49766 80245 2
-60305 -50109 -19924 -39826 50164 79998 2
-59685 -50298 -20185 -40290 50064 80031 2
-60058 -49770 -19797 -39723 50264 79905 2
-60086 -50270 -20295 -39966 49952 79811 2
-60242 -50297 -19864 -39912 50026 79763 2
-60182 -49847 -19852 -40248 50300 80219 2
-60323 -49975 -19938 -40022 50089 80030 2
-59887 -50264 -20021 -39942 49989 80128 2
-60013 -50009 -19712 -40078 50279 79970 2
-60230 -50189 -20161 -39877 49789 80258 2
-59801 -49752 -19762 -40106 49939 80137 2
-60060 -49939 -19840 -39667 49798 80047 2
-59824 -50003 -20212 -39829 50087 79837 2
20298 -223 50131 -20258 40261 60312 3
19952 319 50188 -19668 40065 59729 3
20173 101 49884 -19691 40265 59765 3
20151 -139 50047 -20042 39961 59767 3
20022 277 50019 -20188 39760 60234 3
20190 -99 50259 -20245 39733 59760 3
19878 -110 50054 -20268 39999 60062 3
19957 132 50115 -20236 40017 60040 3
19947 -72 49878 -19977 39965 59765 3
20277 96 50130 -19689 39928 60317 3
19864 44 49724 -20230 39761 60208 3
20184 14 49809 -19780 39782 59962 3
19703 66 50096 -20272 39896 59803 3
20092 -224 50160 -20136 40152 60172 3
20208 -151 49872 -19777 39904 60283 3
19992 292 49900 -20181 40083 59919 3
19738 228 50223 -20255 39803 59736 3
19983 108 49796 -19799 40260 60131 3
20284 207 50174 -19752 40099 60261 3
20061 -74 49859 -20269 40313 59710 3
19827 51 50215 -19946 39801 60060 3
19986 -102 49963 -20078 40184 59880 3
20069 295 50254 -19976 40251 60314 3
20292 35 49853 -19847 40329 60322 3
20122 196 49772 -19668 39840 60287 3
20211 253 50088 -19901 40147 59674 3
20331 -86 50085 -19875 39879 60208 3
19830 251 49949 -19839 40011 60333 3
19745 149 50176 -19901 40033 60155 3
19732 -179 49743 -20292 40240 59986 3
19774 317 49862 -20230 39791 59718 3
19802 287 49877 -20158 40307 60306 3
19889 171 50032 -19890 40035 59773 3
19991 229 49744 -20088 39875 60050 3
20164 84 50167 -20174 40062 60168 3
20215 -255 49769 -20180 40109 60143 3
19890 -10 49821 -20311 40066 59909 3
19829 44 50200 -20172 39988 59967 3
19865 -298 50139 -19956 39957 60156 3
19810 -29 49907 -20020 40104 60279 3
20244 281 50275 -20000 39735 59930 3
20141 -198 50089 -20232 40006 59672 3
19827 115 50097 -19787 39955 60230 3
19686 319 49906 -19869 40018 60248 3
20068 97 49913 -20079 40084 60292 3
20018 319 50234 -20174 39886 60254 3
19686 71 49813 -19681 39907 59827 3
20301 114 49682 -20044 40326 59737 3
20272 65 50294 -19862 40260 60016 3
20243 -331 49776 -20238 40209 59948 3
19789 187 49989 -20238 39926 59965 3
19715 101 50134 -19738 39704 60254 3
19708 -258 49973 -20012 40287 59985 3
20303 -185 49861 -20081 40211 59866 3
-59787 -69961 -29943 40058 -20135 -99983 4
-59828 -70177 -29965 40272 -19770 -100169 4
-59933 -69745 -29778 40209 -20262 -99700 4
-59713 -69682 -30141 40216 -19872 -99774 4
-60043 -70023 -29984 40191 -20269 -99725 4
-59992 -70271 -30222 40079 -20054 -99994 4
-59836 -70273 -30022 40328 -20196 -100294 4
-60322 -69992 -29680 39918 -20155 -100114 4
-60002 -70015 -30323 40230 -20156 -100127 4
-60194 -69760 -30329 39906 -20288 -100278 4
-59832 -70148 -29699 39719 -20003 -100252 4
-59732 -69871 -30125 39783 -20045 -100071 4
-59868 -70007 -29917 40326 -20118 -100139 4
-60325 -70290 -29807 39910 -20184 -100259 4
-60233 -70116 -29843 40000 -20173 -99952 4
-59904 -70288 -29680 40321 -20154 -99829 4
-60029 -70056 -29689 39898 -20002 -99989 4
-60268 -69992 -29699 40143 -19937 -99683 4
-59744 -70179 -29877 40022 -20272 -99773 4
-60201 -69817 -30184 40299 -20226 -99779 4
-59800 -69812 -29939 39973 -19910 -99803 4
-59898 -70159 -30263 40112 -20139 -99672 4
-60041 -69853 -30329 40315 -19861 -100050 4
-59898 -70244 -29798 39727 -19907 -99952 4
-59815 -70027 -29850 40250 -19948 -100307 4
-59722 -70244 -30124 39710 -19901 -100210 4
-59928 -70137 -29833 40027 -19992 -100210 4
-59742 -69926 -30293 39945 -20071 -99869 4
-59729 -69836 -30042 39690 -19854 -99709 4
-60040 -69689 -29788 39929 -20036 -100328 4
-59702 -69909 -29978 40144 -19683 -100266 4
-60183 -70244 -29842 39696 -19832 -100141 4
-60122 -69895 -30119 39884 -20172 -100040 4
-59722 -69977 -30015 40013 -20080 -100013 4
-60296 -70277 -30111 40306 -19867 -99807 4
-59736 -70266 -29998 39740 -19730 -99842 4
-59988 -70316 -30071 40296 -20087 -100151 4
-59758 -69832 -30048 39812 -19920 -100298 4
-60305 -69842 -29976 39834 -20206 -100120 4
-60096 -70234 -29684 40272 -20218 -99812 4
-60255 -70194 -29901 40032 -19962 -100170 4
-59847 -69933 -30319 39971 -20103 -100232 4
-59860 -69772 -29964 39677 -20292 -100183 4
-60283 -69762 -29965 39804 -19736 -99803 4
-60017 -69837 -29921 39932 -19748 -100323 4
-59982 -70006 -30242 40305 -19836 -100332 4
-59976 -69884 -29684 40129 -19814 -100132 4
-59923 -70096 -29688 39909 -19737 -100324 4
-59833 -69826 -30050 40194 -19746 -99891 4
-60148 -69686 -29944 40197 -20132 -100050 4
-60025 -69847 -29998 40030 -20079 -99931 4
60178 -59956 -20289 -9680 10136 208 5
59785 -60315 -20208 -10216 10188 -269 5
59694 -60095 -19949 -9967 9997 164 5
59787 -59724 -19918 -9692 10018 -136 5
59998 -60251 -19888 -10178 9951 -255 5
60168 -59908 -19854 -10127 10021 -89 5
60077 -59956 -20218 -10006 9890 -66 5
59956 -59789 -20171 -9859 10049 -28 5
59687 -60296 -19699 -10029 10046 -99 5
59835 -59689 -20000 -9821 9741 253 5
59679 -59897 -19707 -10235 10133 185 5
60176 -59670 -20118 -10096 9747 330 5
60259 -60159 -19969 -9671 10228 303 5
60229 -60333 -20182 -9735 9736 169 5
59982 -60235 -20309 -9990 9667 -310 5
60216 -60206 -19735 -10314 9768 241 5
59953 -60120 -19689 -9942 10200 175 5
60265 -60214 -19967 -10078 9916 47 5
60180 -60219 -19886 -9951 9669 -286 5
59860 -59819 -20251 -9731 10182 106 5
60288 -60323 -19993 -10212 10140 249 5
59788 -59985 -19787 -9674 10180 324 5
60054 -60093 -19916 -10026 10264 -24 5
60037 -59874 -19899 -9718 10214 203 5
59975 -59780 -20304 -10209 10161 -158 5
60002 -60110 -19773 -10332 9723 38 5
60263 -59812 -20036 -9791 10018 19 5
60190 -60189 -19867 -9667 10132 -181 5
59807 -60244 -20255 -10156 10330 98 5
59777 -59888 -20260 -10104 9820 171 5
60323 -59985 -20181 -10186 9934 177 5
59969 -59690 -20329 -10160 9695 -309 5
59853 -59859 -19836 -10157 9777 288 5
60110 -60331 -19794 -10066 10046 -187 5
60045 -59836 -20323 -10147 9905 256 5
59951 -59831 -19667 -9836 10188 -62 5
60298 -60111 -19860 -10216 9931 293 5
60245 -59921 -20158 -9905 9791 298 5
59954 -60286 -20278 -9671 10186 -71 5
60306 -60333 -19899 -9995 9872 86 5
60147 -60073 -19852 -10147 9786 -143 5
60297 -59940 -19811 -9715 10061 79 5
60110 -60015 -20210 -10279 9857 240 5
60204 -59918 -19686 -9680 10104 -171 5
59890 -59926 -19771 -10075 9754 148 5
60250 -59892 -20012 -9701 9886 42 5
60268 -60262 -19873 -9753 9750 330 5
59872 -59782 -19832 -9872 9972 -209 5
59816 -59709 -19830 -10023 10089 -124 5
60257 -59831 -20228 -10049 10184 291 5
60286 -59995 -19893 -9923 9845 332 5
60247 -59694 -20111 -10184 9945 329 5
60007 -59700 -20284 -9819 10157 172 5
60236 -60274 -20020 -9893 10002 228 5
59997 -60287 -19683 -9914 9828 257 5
59788 -59825 -19847 -10296 10123 317 5
29939 -100196 89831 59698 -80311 49889 6
29953 -99775 89710 60246 -79692 50001 6
30107 -100254 90099 59876 -80167 50137 6
29702 -100166 89941 59901 -80333 50072 6
29821 -99756 89802 60261 -79954 49882 6
30054 -100216 90110 60232 -80016 50272 6
29854 -100155 89801 59964 -79668 50188 6
30132 -99969 89987 60263 -79698 50284 6
29829 -99765 89806 60169 -79698 50218 6
30097 -99920 89697 59847 -79757 49868 6
29709 -99921 89697 59720 -79779 49846 6
30019 -99745 89719 60257 -79737 49995 6
29996 -99950 90240 59747 -79894 49788 6
29967 -99809 90016 60008 -79859 49784 6
30197 -100238 89839 59815 -79886 49935 6
30327 -99690 89685 59769 -79696 50267 6
29725 -99805 89833 59694 -79995 49731 6
30294 -99731 90246 60193 -79706 49680 6
30164 -99919 89729 60331 -79975 49770 6
30138 -99962 90161 59741 -79684 50052 6
30070 -99745 90161 59884 -79895 50193 6
29795 -100011 89673 59863 -79835 50009 6
29732 -100213 90032 59697 -80184 49798 6
29911 -100182 90199 60113 -79976 50017 6
30079 -100110 90189 59909 -79710 50310 6
30317 -99681 90174 60194 -79970 49805 6
29891 -99949 90267 60282 -80167 49671 6
29999 -100032 90067 59817 -80181 49765 6
30065 -99740 90045 60069 -79769 50330 6
29897 -100125 89676 59894 -79688 50045 6
29823 -99688 90028 60286 -80327 50119 6
30225 -99958 89910 59989 -80207 49683 6
30143 -99714 90259 60187 -80188 50031 6
29825 -99933 89769 60230 -79711 50066 6
29974 -100255 90206 60137 -79692 50243 6
30240 -99778 89931 60111 -79962 49848 6
30127 -100205 89877 59937 -80201 49933 6
29794 -100075 90315 60047 -79825 50053 6
30004 -99671 90065 59761 -79757 50204 6
30187 -99700 89808 60290 -80169 50097 6
30126 -99836 89947 59712 -79779 50224 6
29864 -100207 89750 59959 -79730 49844 6
30065 -99762 89693 59688 -79911 49944 6
30089 -99859 90183 60158 -80101 49812 6
30031 -100332 90243 60215 -79976 49785 6
30011 -99961 90075 60181 -79818 49734 6
30060 -99688 89817 60103 -79748 49914 6
29863 -99901 89744 60283 -80096 50296 6
30116 -100285 89952 59996 -79844 50017 6
30271 -100060 90107 60017 -79745 49894 6
29691 -100189 90013 60169 -79918 49755 6
29750 -100231 90200 60008 -80132 50024 6
29936 -100123 89790 60242 -79885 49856 6
30025 -100011 90215 60036 -80069 49695 6
29903 -99825 90030 60145 -79926 50249 6
29885 -99764 89764 60218 -79988 50147 6
29939 -99694 89671 59810 -79836 50297 6
29894 -100020 89705 59746 -79958 50333 6
49809 -103 10169 19756 -39995 -10155 7
49750 80 9787 19885 -39801 -10312 7
49668 231 9914 19904 -40247 -10034 7
50036 -234 9697 20213 -40208 -9673 7
49920 -33 10224 20226 -40140 -10065 7
50168 -24 10143 20171 -39889 -10114 7
49862 269 9668 19726 -40268 -10114 7
50242 -235 9668 19691 -40147 -10322 7
50254 247 10054 19668 -39905 -9913 7
49725 179 9734 20060 -39996 -9896 7
50163 90 9770 20311 -39950 -9899 7
50064 205 9840 20023 -40210 -10242 7
49953 286 9974 20175 -39948 -9691 7
50169 55 10310 20206 -39790 -9919 7
50272 -241 9900 19714 -40061 -10325 7
50055 195 9787 19807 -39983 -9728 7
50028 71 9712 19700 -39811 -9832 7
49785 -146 10050 19914 -40316 -10203 7
50202 38 9778 20258 -40248 -9710 7
50080 -175 9772 19850 -40329 -10091 7
49927 190 10233 19866 -39918 -9908 7
49812 -5 10180 19745 -40280 -10030 7
50149 307 9983 19874 -39696 -9864 7
49826 124 9969 20234 -39745 -10188 7
50333 307 10245 20100 -39842 -9905 7
49823 -297 10240 20175 -39903 -9835 7
50113 299 9751 20321 -40086 -10326 7
50012 -228 9897 20010 -39970 -10261 7
49941 -170 9847 20133 -39964 -9900 7
49844 139 10279 19852 -40083 -9864 7
50279 93 9885 20071 -40187 -10052 7
49911 -200 10144 20245 -39882 -10318 7
49823 245 9676 20045 -39764 -10020 7
50118 -158 10254 20128 -40098 -10124 7
49754 111 10048 19860 -40162 -9983 7
50075 -64 10306 19865 -39977 -9809 7
49944 -109 10213 19762 -39727 -9761 7
50005 -185 9939 19745 -40300 -9840 7
49936 280 9913 20242 -40008 -9910 7
49986 294 10331 20093 -39880 -10150 7
49674 213 10177 19992 -39911 -10120 7
50280 -333 10129 20038 -40283 -10303 7
49840 89 10035 19966 -40061 -10100 7
50319 79 10260 20278 -39674 -9805 7
50132 -317 9985 19708 -39671 -10027 7
50149 328 10154 19726 -39859 -10318 7
50113 -158 9931 20081 -39723 -9835 7
50206 -48 9933 20238 -40029 -9974 7
50121 24 10235 20073 -39989 -9726 7
50198 -254 10228 19775 -39844 -10063 7
49697 -24 9751 20145 -40099 -10163 7
50313 -124 9674 20309 -39918 -10134 7
50226 -143 9841 19890 -40002 -9802 7
50199 -74 10310 20179 -39768 -10109 7
49757 213 10074 20293 -39763 -9845 7
50325 -244 9956 19716 -39766 -9857 7
49805 -21 10212 20189 -39692 -9726 7
49743 285 10213 19938 -40163 -9922 7
50041 -269 10303 19734 -40056 -9953 7
-20311 -333 -10225 -100005 29937 -50325 8
-19764 323 -9955 -100128 29744 -49743 8
-20033 241 -10206 -99731 29686 -49754 8
-20026 26 -9785 -100030 30252 -49883 8
-20051 -200 -9769 -100312 29835 -50103 8
-19711 -31 -9926 -100196 29846 -49867 8
-20311 230 -10017 -99978 29867 -49986 8
-19939 -270 -9739 -99733 30099 -49862 8
-19866 -196 -9969 -99978 30273 -49924 8
-20088 -35 -9867 -100314 30011 -49863 8
-19752 46 -10222 -100280 30013 -50320 8
-19752 68 -10236 -100195 30140 -49957 8
-19851 182 -9865 -99879 29909 -49968 8
-20312 -104 -10171 -100214 29719 -49748 8
-19889 92 -10238 -99987 30302 -49819 8
-20282 298 -10227 -99920 30240 -50223 8
-19768 -127 -9844 -100276 30139 -49780 8
-19813 -76 -9765 -100122 30294 -49685 8
-20196 196 -10137 -99989 30329 -49675 8
-19787 58 -10315 -99712 29702 -50153 8
-20006 -61 -10125 -99830 30209 -50035 8
-19780 -195 -9864 -100072 30081 -49977 8
-20081 -234 -9875 -100127 29969 -49760 8
-19943 -247 -9776 -100314 30113 -49670 8
-20324 174 -9759 -100091 29936 -50292 8
-20061 -41 -9984 -100205 30070 -49895 8
-19861 -71 -10073 -99938 30115 -50151 8
-19901 300 -9979 -99705 29899 -49784 8
-20005 218 -9738 -99963 29761 -50071 8
-20074 208 -9814 -99945 30272 -49670 8
-19819 165 -9955 -100005 29831 -49780 8
-20072 102 -9976 -99869 30060 -49968 8
-19760 -153 -9823 -99963 29707 -49969 8
-19894 -275 -10237 -100065 30269 -50015 8
-19823 -32 -10149 -100046 29804 -49828 8
-19720 170 -9782 -100088 30064 -50192 8
-20043 24 -10176 -100223 29721 -50309 8
-20160 235 -10101 -100301 30231 -50270 8
-20232 166 -9880 -100036 30160 -50019 8
-20166 228 -9761 -99678 29685 -49740 8
-19749 -153 -9831 -100055 29826 -50251 8
-19901 315 -10327 -99942 29858 -50304 8
-20157 312 -9704 -99759 29909 -49686 8
-20332 -117 -9798 -99705 30115 -50105 8
-19874 155 -10281 -99899 29953 -49827 8
-19678 -227 -10061 -100032 30309 -50332 8
-20044 38 -10150 -99746 30319 -49755 8
-20017 -9 -9692 -100326 30282 -50087 8
-20320 317 -9905 -100110 29837 -50055 8
-20293 -129 -10108 -99739 29798 -50124 8
-20078 -272 -10042 -99743 30072 -49869 8
-19672 92 -10030 -99961 30065 -50322 8
-60210 -50084 50223 59726 30222 -96 9
-60041 -50222 50027 59955 30250 -251 9
-60323 -50109 49824 60111 29908 274 9
-59908 -49792 49738 60155 29819 249 9
-60083 -50322 50010 60293 29921 -250 9
-60039 -49996 50193 60294 30325 59 9
-59936 -50323 49748 60112 30078 -225 9
-59837 -49779 49794 60141 29893 283 9
-59774 -49923 49754 59928 30306 -106 9
-60035 -50060 49952 60267 30290 105 9
-59790 -49934 49963 59993 30301 -219 9
-59896 -49969 50011 59709 29889 -133 9
-59955 -49839 49980 60269 30029 -141 9
-59981 -50297 49706 59949 29712 -40 9
-60018 -50297 50159 60211 30150 301 9
-60276 -49746 49767 60098 30250 20 9
-60191 -49993 49775 59829 30209 -240 9
-60067 -49680 50181 60077 30087 307 9
-59930 -50179 49879 59984 29890 -182 9
-59765 -50066 49749 60179 30190 -140 9
-59956 -50317 50252 59827 29683 137 9
-59862 -50207 50121 59920 29849 -243 9
-59738 -49718 49979 59931 30109 -213 9
-60299 -50145 50050 59866 29794 22 9
-59939 -50168 50221 60115 29788 270 9
-60115 -50182 49784 60079 29877 -166 9
-59819 -49990 50226 59709 30282 -30 9
-59854 -49807 50206 60173 30013 131 9
-60064 -49740 50123 60010 29827 -165 9
-59894 -49686 50283 60251 30127 192 9
-60013 -50205 49857 60129 29909 -18 9
-59896 -50002 49704 60054 29865 -165 9
-60007 -50141 49728 59885 29828 -229 9
-60085 -50298 50313 59811 29815 167 9
-60037 -50259 49864 60047 29985 -321 9
-59745 -50184 50231 59762 29753 170 9
-60201 -49715 50141 60283 29769 -237 9
-59859 -50241 49883 60169 30061 293 9
-60092 -49709 49912 59875 29700 182 9
-59943 -50228 49745 59860 30037 -121 9
-60098 -49843 50005 60104 29999 -178 9
-59705 -50121 49757 59721 30072 246 9
-60306 -49728 49963 60098 29969 -332 9
-60045 -50313 49712 59754 30246 293 9
-59814 -49858 49960 60125 29790 203 9
-60101 -49708 49718 59909 29687 124 9
-59861 -50280 49869 59952 29709 77 9
-60169 -50054 49719 59960 30333 -271 9
-59851 -49947 49882 60110 29706 -209 9
-59996 -50174 49751 60298 29893 66 9
-59892 -50062 49919 60076 30147 -304 9
-60198 -50054 49918 59900 30125 127 9
-60191 -49675 49849 60299 30067 -31 9
-60048 -49735 49990 59858 30141 5 9
-60164 -50213 49856 60080 29839 -47 9
-59776 -49747 50327 60296 30037 96 9
-59799 -49884 49688 60265 30208 -322 9
-59882 -50055 50231 59725 29863 -242 9
-59803 -49970 49691 59874 30102 -119 9
-60321 -50313 50219 60211 30120 -318 9
Visualize Data¶
Does the test case generate produce the data with expected properties? One way to answer this question is to visualize data (up to three dimensions). Visualization can help inspect whether the data produced by the test generator is indeed clustered into several regions.
#! /usr/bin/python3
# visualize.py
# Visualize test cases for k-mean clustering program
# up to the third dimension
import sys
import matplotlib.pyplot as pyplot
from mpl_toolkits.mplot3d import Axes3D
def visualize(infile):
try:
fin = open(infile, 'r')
except:
sys.exit('open fail')
# fine the maximum and minimum values
# up to the first three dimensions
# initialize the minimum values
minval = sys.maxsize
maxval = - sys.maxsize
xval = []
yval = []
zval = []
for oneline in fin:
numbers = oneline.split()
# get the number of dimensions
dim = len (numbers)
# consider up to the first three dimension
for ind in range(0, min(3, dim)):
if (ind == 0):
xval.append(int(numbers[ind]))
if (ind == 1):
yval.append(int(numbers[ind]))
if (ind == 2):
zval.append(int(numbers[ind]))
minval = min(int(numbers[ind]), minval)
maxval = max(int(numbers[ind]), maxval)
# print (minval, maxval)
if (dim == 1):
yval = [0] * len(xval)
if (dim <= 2):
pyplot.scatter(xval, yval)
if (dim >= 3):
fig = pyplot.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(xval, yval, zval)
pyplot.show()
if __name__ == "__main__":
input = 'data.txt'
visualize(input)
TODO: explain the code
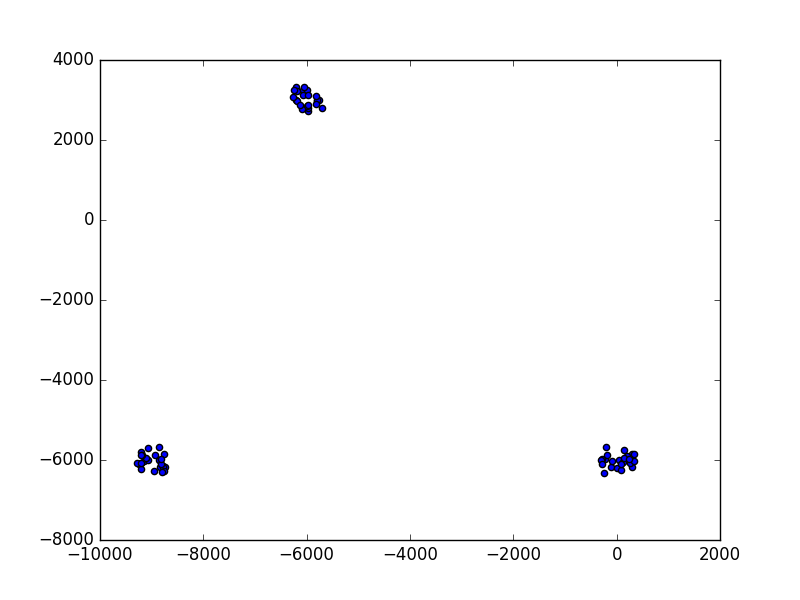
Visualize a generated test case of three clusters, clearly separated.
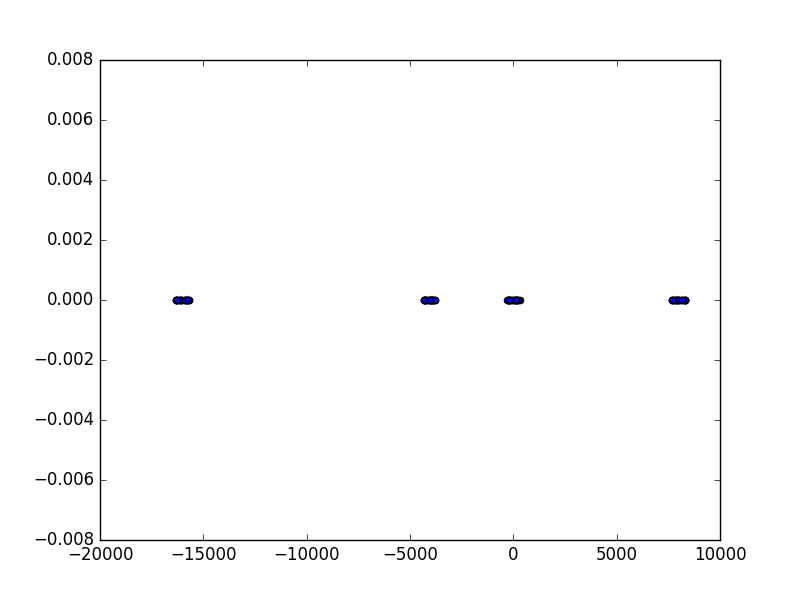
Figure 38 A test case generated with -d 1 -m 4 arguments.¶
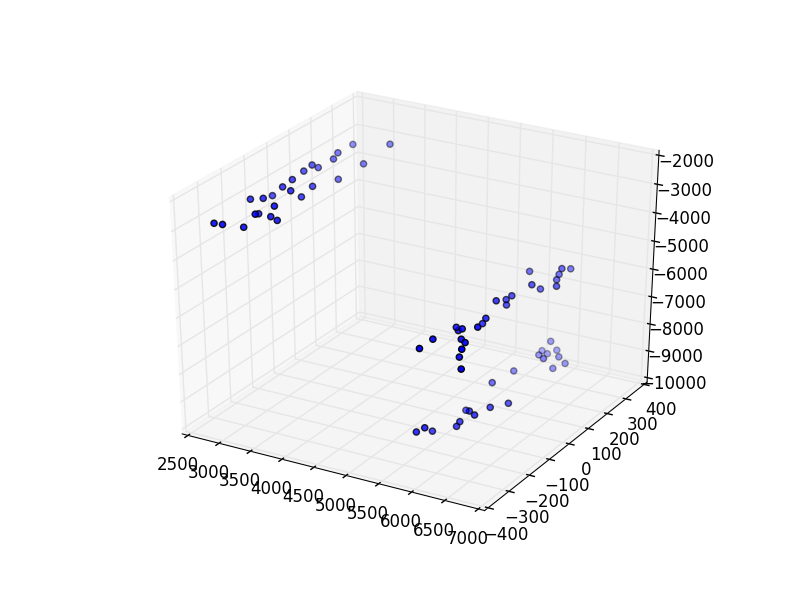
Figure 39 A test case generated with -d 3 -m 3 arguments.¶
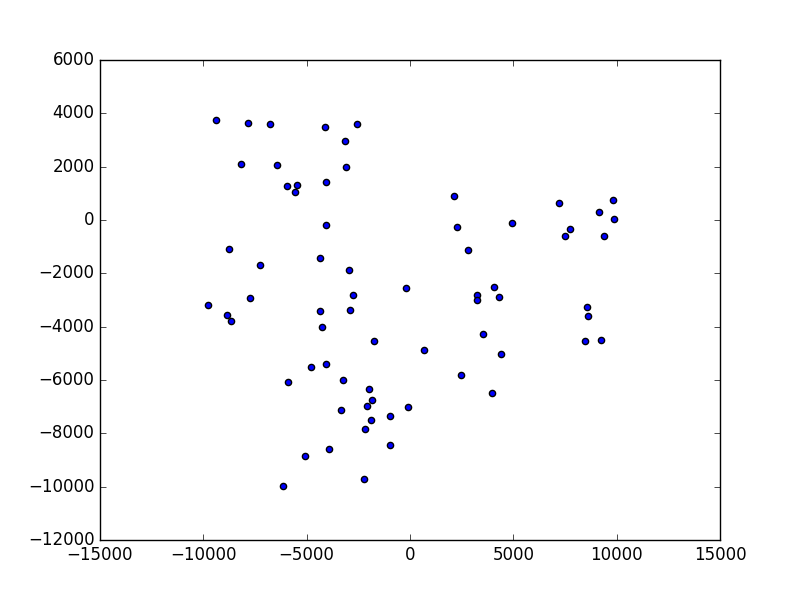
Figure 40 A test case generated with -t -m 3 arguments.¶
K-Mean Implementation¶
Now is the time to show how the K-Mean algorithm can be implemented. The implementation pretty much reflects the algorithm described earlier.
TODO: Explain the program
#! /usr/bin/python3
# main.py for kmean
import sys
import kmean
import argparse
def checkArgs(argv = None):
parser = argparse.ArgumentParser(description='parse arguments')
parser.add_argument('-k', '--kval', type = int)
parser.add_argument('-f', '--filename',
help = 'name of the data file', default = 'data.txt')
parser.add_argument('-s', '--summary', type = bool,
help = 'summary of result', default = False)
args = parser.parse_args(argv)
return args
if __name__ == "__main__":
args = checkArgs(sys.argv[1:])
kmean.kmean(args)
# kmean.py
import sys
import random
from datapoint import DataPoint
from centroid import Centroid
def distance(datapoint, centroid):
sum = 0
dim = datapoint.getDimension()
for ind in range(0, dim):
val1 = datapoint._data[ind]
val2 = centroid.data[ind]
diff = val1 - val2
sum = sum + diff * diff
return sum
def cluster(dataArray, kval):
numdp = len(dataArray)
centroidArray = []
dim = dataArray[0].getDimension()
for ind in range(0, kval):
ctd = Centroid(dim, ind)
centroidArray.append(ctd)
done = False
while (done == False):
done = True
for cluindex in range(0, kval):
centroidArray[cluindex].reset()
# calculate the centroid of each cluster
for dpindex in range(0, numdp):
clu = dataArray[dpindex].getCluster()
centroidArray[clu].addPoint(dataArray[dpindex])
for cluindex in range(0, kval):
centroidArray[cluindex].findCenter()
# find the closet centroid
for dpindex in range(0, numdp):
mindist = sys.maxsize # minimum distance so far
minclu = -1
for cluindex in range(0, kval):
dist = distance(dataArray[dpindex], centroidArray[cluindex])
if (mindist > dist):
mindist = dist
minclu = cluindex
curclu = dataArray[dpindex].getCluster()
if (curclu != minclu):
# this data point is assigned to a different cluster
done = False
dataArray[dpindex].changeCluster(minclu)
return centroidArray
def readfile(fhd, kval):
dataArray = []
for oneline in fhd:
# assign each data point to a cluster randomly
clu = random.randint(0, kval - 1)
data = list(map(int, oneline.split()))
dp = DataPoint(data, clu)
dataArray.append(dp)
return dataArray
def printSummary(dataArray, centroidArray, kval):
# print in the format of a CSV file
# kval, distance (cost), sizes of clusters
# calculate the number of data points in each cluster
line = str(kval)
clustersize = [0] * kval
numdp = len(dataArray)
# calculate the value of the cost function
dist = 0
for dpindex in range(0, numdp):
clu = dataArray[dpindex].getCluster()
dist = dist + distance(dataArray[dpindex], centroidArray[clu])
line = line + ',' + str(dist)
for dpindex in range(0, numdp):
clu = dataArray[dpindex].getCluster()
clustersize[clu] = clustersize[clu] + 1
for clu in range (kval):
line = line + ',' + str(clustersize[clu])
print (line)
def kmean(args):
# print (args)
filename = args.filename
kval = args.kval
summary = args.summary
try:
fhd = open(filename)
except:
sys.exit('open fail')
dataArray = readfile(fhd, kval)
fhd.close()
numdp = len(dataArray)
# for dpindex in range(0, numdp):
# dataArray[dpindex].printData()
# print ('-------------------------------')
centroidArray = cluster(dataArray, kval)
# print ('+++++++++++++++++++++++++++++++')
if (summary):
printSummary(dataArray, centroidArray, kval)
else:
for dpindex in range(0, numdp):
dataArray[dpindex].printData()
# datapoint.py
# each object has two attributes:
# data (an array) and
# which cluster it belongs to (an integer)
class DataPoint:
def __init__(self, dat, clu):
self._data = dat # assign only once, read only
self.cluster = clu
def changeCluster(self, newclu):
self.cluster = newclu
def getData(self):
return self._data
def getDimension(self):
return len(self._data)
def getCluster(self):
return self.cluster
def printData(self):
print (self._data, self.cluster)
# centroid.py
class Centroid:
def __init__(self, dim, id):
if (dim <= 0):
print ('Invalid Number of Dimension')
return
self._dim = dim # assign once, read only
self._ID = id # assign once, read only
self.reset()
def reset(self):
self.size = 0 # number of data points in this cluster
self.data = [0] * self._dim
def addPoint(self, point):
dim = len(self.data)
if (dim != point.getDimension()):
print ('Wrong Dimension')
return
for ind in range(0, dim):
self.data[ind] = self.data[ind] + point._data[ind]
self.size = self.size + 1
def findCenter(self):
if (self.size == 0):
# print ('Centroid', self._ID, 'Without Data')
return
for ind in range(0, self._dim):
self.data[ind] = self.data[ind] / self.size
Does this program work? Let’s try an example.
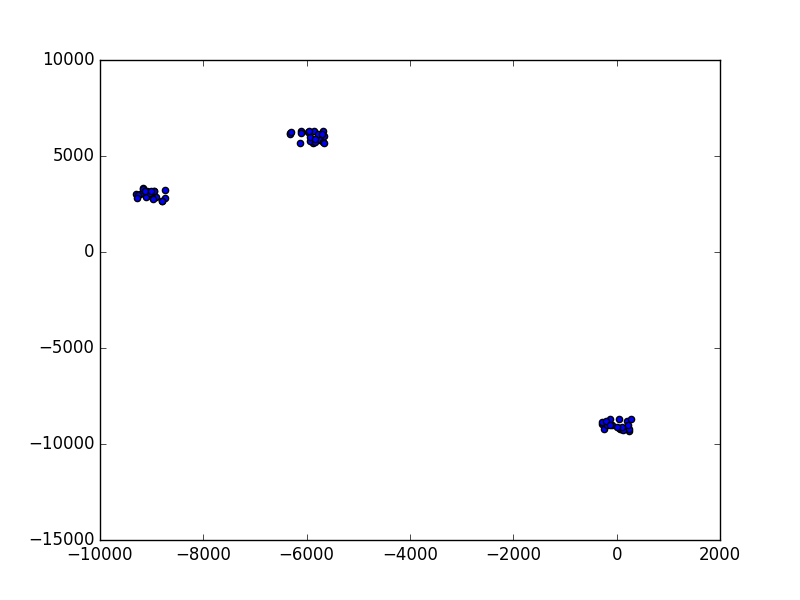
Figure 41 A generated test case.¶
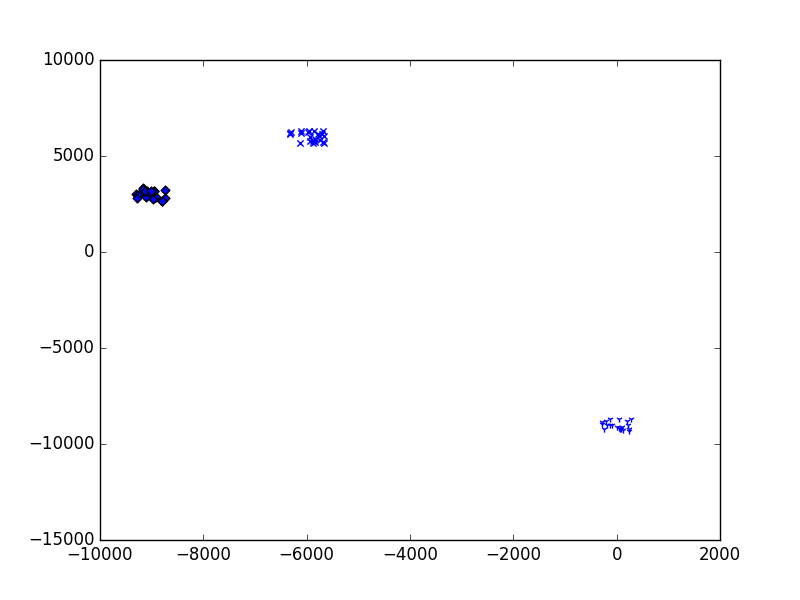
Figure 42 The clusters are marked by different labels. The result is encouraging.¶
Next, consider some more test cases:
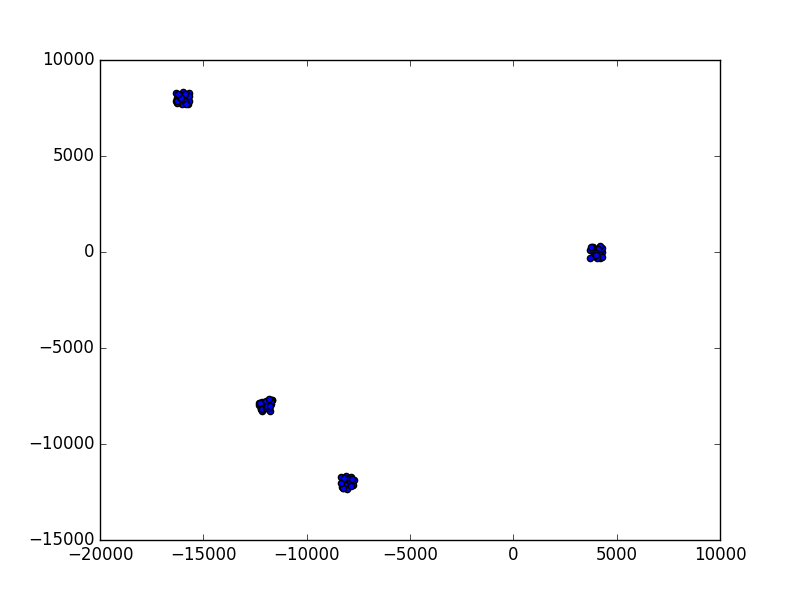
Figure 43 A test case generated with -m 4 arguments.¶
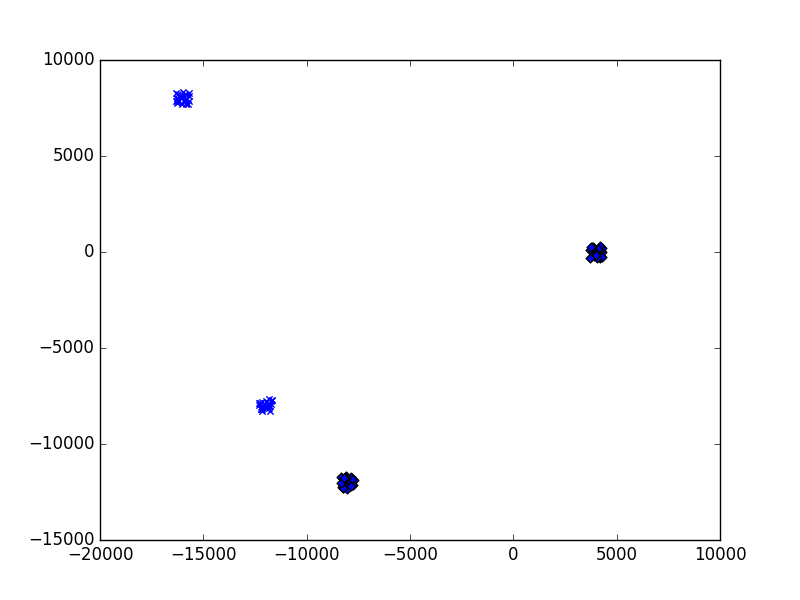
Figure 44 K-mean result using only two clusters.¶
The next example allows clusters to overlap by adding -t in
the test generator.
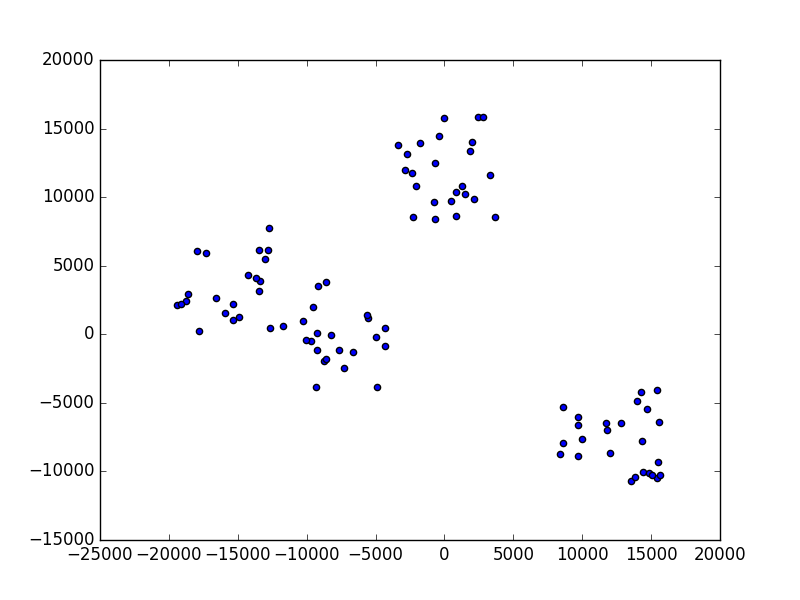
Figure 45 A test case generated with -t -m 4 arguments.¶
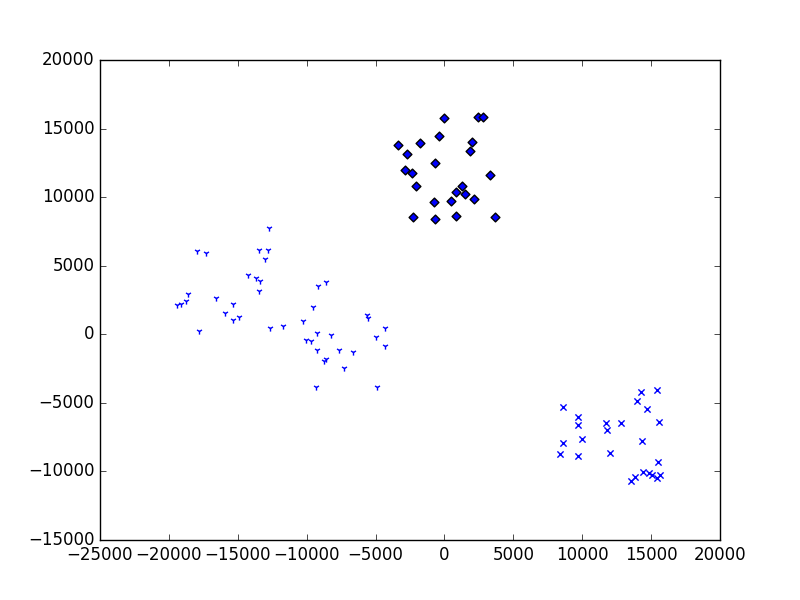
Figure 46 K-mean result using three clusters.¶
This looks pretty good. Running the same clutering multiple times, we may get different results:
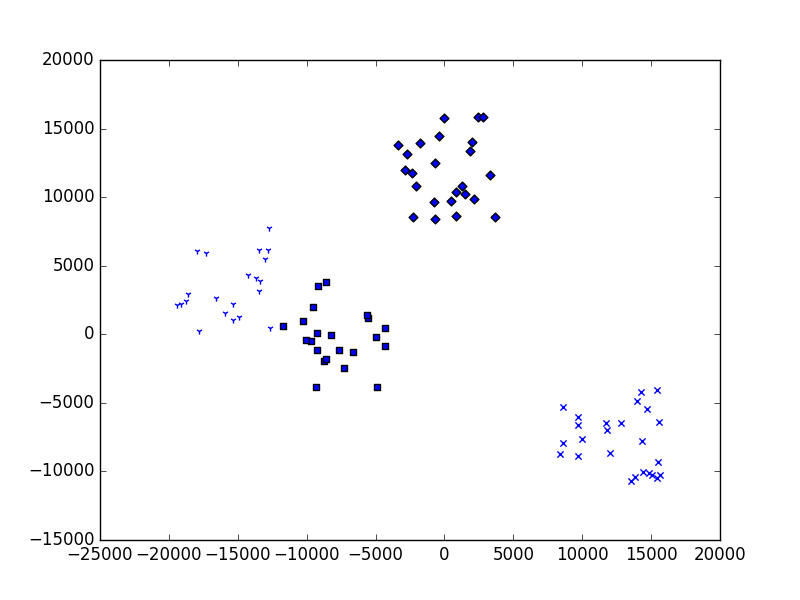
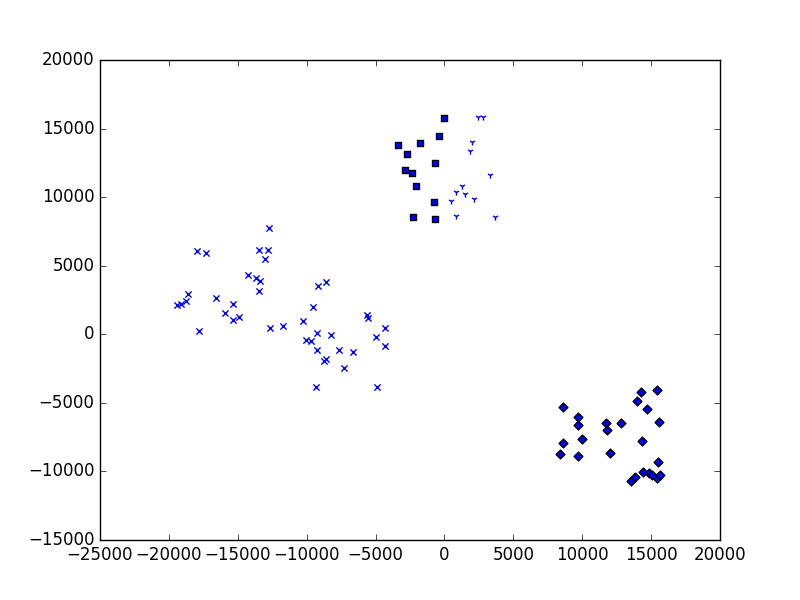
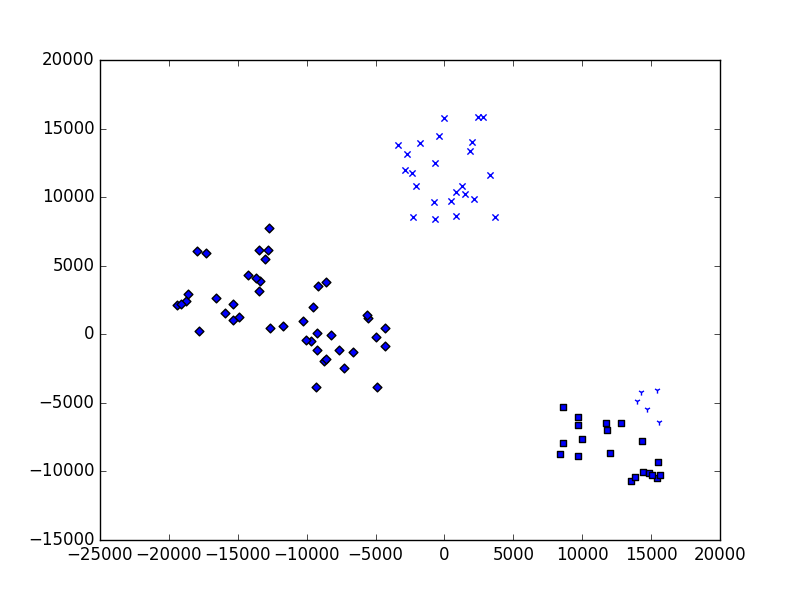
Figure 47 Running the program three times using four clusters.¶
The top one seems reasonable but the other two are questionable. Why?
Understand Non-Deterministic Behavior of K-Mean¶
This is the place where most books stop and why this book is unique. This book gives deeper insight.
How can this program produces different results even though the input data is the same? A simple answer is that this program is non-deterministic because of this line
clu = random.randint(0, kval - 1)
It assigns each data point to a cluster between 0 and k-1
randomly. It is possible that two or more data points in the same
cluster (by the test generator) are assigned to different clusters.
Python (and most programming languages) has a random number
generator. It would be difficult to predict the next number after
observing a sequence of numbers. Let us consider several
examples. This is a simply program calling Python’s random.randint.
# sequence1.py
import datetime
import random
if __name__ == "__main__":
for cnt in range(10):
print (random.randint(0, 100000))
# print a number between 0 and 100000
# 0 and 100000 are possible
The following shows the results executing the program three times.
97539
86848
83989
96528
90232
11563
23388
27759
45757
35145
48460
72777
83220
87378
76795
97287
29736
73663
19199
28427
83797
42300
7057
9665
51669
57868
72789
20256
40249
47526
It is difficult to predict the next number from the numbers that have already been seen. Python allows programmers to set the seed of the random number generator. If the same seed is same, the same sequence of numbers is generated. In other words, the sequence becomes deterministic. The following program always generates the same sequence of numbers.
# sequence2.py
import datetime
import random
if __name__ == "__main__":
random.seed(1)
for cnt in range(10):
print (random.randint(0, 100000))
The words “random” and “non-deterministic” are often confused. Random
means it is difficult to predict in advance. Non-deterministic means
that if the same program runs again with the same inputs, the results
may be different. It is possible to have a deterministic sequence of
random numbers, like the ones generated by sequence2.py. The
sequence is deterministic because running the program again generates
the same sequence. The sequence is random because knowing the
generated numbers cannot predict the future numbers.
Another common confusion is “random” and “unknown”. If a sequence of number is random, the next unseen number is unknown (unless the seed is set). However, something that is unknown may not be random. For example, you may not know the birthday of a person but this person’s birthday is not “random”.
A common way of varying the seed is using the microsecond of the current time in the following way:
random.seed(datetime.datetime.now().microsecond)
Be careful using time as random number seeds for keys in security
programs. Using microseconds restrict the possible keys to only 0
and 999999, not the full scale of all possible integers.
It is possible that the data points that should be in the cluster are put into different clusters. When this occurs, the results are not very useful. Since the k-mean algorithm does not guarantee finding the best clustering solution, it is advised running the program multiple times and find the result that has the smallest value of the cost function.
Determine k’s Value¶
One important question is to determine the value of k. This can
also be answered by using different values and choose one that
minimize the cost function. The following function considers
different values of k and runs the program multiple times for each
value.
Consider the data generated using -d 6 -c 10 -m 50 -M 60 as the
input. The following figure shows the sum of the distances to the
centrolds for different values of k. It is clear that when k
is too small (below 8), the distances are much larger.
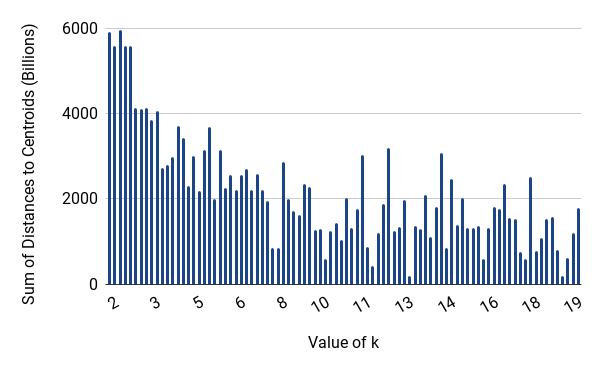
Figure 48 Distances for different values of k. Five times for each value.¶
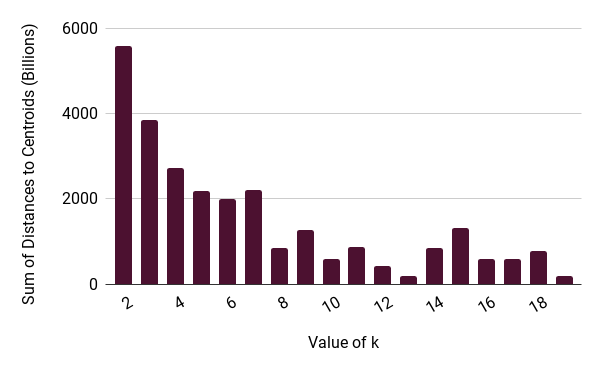
Figure 49 Smallest distance for each value. Please notice that the smallest distance occurs when k is 13. The data is generated for 10 clusters.¶
Each value runs five times and has five bars. The size of each cluster
is shown as the height. Since the clusters together contain all data
points, the sum of the cluters’ sizes is always the same. The
sizes of the clusters can vary significantly. For example, when k
is 5, the smallest cluster has no data point and the largest cluster
has more than one third of the data points.
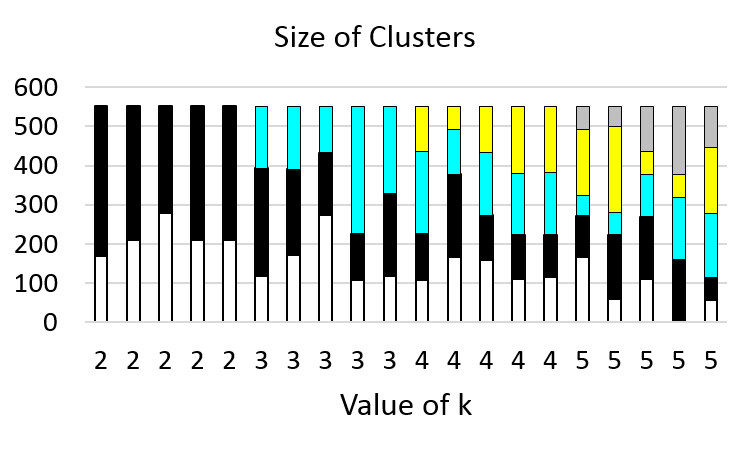
Figure 50 Sizes of clusters for different values of k.¶
Clean Data before Clustering¶
The k-mean algorithm seems relatively simple. Is it actually useful?
Yes. The beginning of this chapter describes several scenarios where
clustering would be helpful. Here are some other applications.
Imagine that you own several pizza stores and want to open new stores.
You want to decide the new stores’ locations. You have the budget to
open at most five more stores (in this case k is between 1 to 5).
You want to use the addresses of deliveries to determine the stores’
locations as the centroids of the clusters based on customers’
addresses. This can be applied to many other scenarios: As another
example, a bank wants to decide where to install four ATM (automatic
teller machine) machines (k is 4 in this case) based on customers’
home and office addresses. Both of them can take advantage of the
clustering method.
It is common that the data needs to be “cleaned” before sending to a clustering program. For example, if you want to decide the locations of pizza stores, you may want to exclude the customers that are too far away from the other customers, maybe more than 10 km away from all the other customers. Maybe you also want to consider how often customers order deliveries and give frequent customers larger weights so that the stores are closer to these customers. The same thinking can be applied to selecting ATM locations: maybe you want to give higher weights to the customers that have high account balances or use ATM more often.
Such “data cleaning” usually requires human judgement. In the example of deciding pizza stores’ locations, should the customers be excluded if they are more than 10km away from all the other customers? Why should it be 10km? Why not 5, or 8, or 15km? If you want to include the customers that order deliveries often even though they live more than 10km away, how do you define “often”? Is more than once per week considered often? Or more than twice per week? Is one week too short? Instead, you prefer to consider ordering more than five times per month? Doing meaningful data cleaning often requires knowledge about the business. You need to know how much it costs to deliver pizza for customers living at different distances from the store. You also need to know the traffic conditions: delivering pizza to a customer living in the center of a city may take longer even though the distance is shorter. The business knowledge is essential understanding what data is needed, what data should be excluded, and how to interpret the results from the clustering method. Using the k-mean method, or any machine learning method, is not as simple as throwing data into a program and get meaningful results effortlessly.
Summary¶
K-Mean is a simple clustering method and it can be the starting point
of more complex methods. It can handle high-dimensional data (even
though visualization above three-dimensional is difficult). When you
get a set of data, you may use K-Mean (experiment with different
values of k) to obtain some idea whether the data is somewhat
clustered.