Hierarchical Clustering¶
Learning Objectives
Understand hierarchical clustering algorithm
Learn the binary tree and its properties
Use the tree’s properties to gain insight of data
Implement the algorithm for hierarchical clustering
Limitations of the k-mean Algorithm¶
The previous chapter explains the k-mean clustering algorithm. It is simple and useful as an initial analysis of data but it also has several major problems:
There is no obvious reason to select a particular value of k. The previous chapter shows an example: the data is generated for 10 clusters but the smallest distance occurs when
kis 13.The algorithm is non-deterministic and it is often necessary running the same program multiple times.
For a given cluster, there is no easy answer which other cluster is closer. It is possible to calculate the distances of centroids but this requires additional work.
The k-mean algorithm assigns all data points to one of the
kclusters in the very first step. Then the algorithm adjusts the clusters by the finding closest centroid from each data point. Because the initial assignments have direct impacts on the final results, the program often needs to run multiple times for selecting better results.
Hierarchical Clustering is a method that does not have these same problems as the k-mean algorithm.
Examples of Hierarchical clustering¶
Hierarchical clustering iteratively finds the closest pair of clusters (at the beginning, each data point is a cluster by itself). The algorithm makes the pair two children of a binary tree. For hierarchical clustering, it is called dendrogram, instead of binary tree. This book uses both terms interchangably. The tree node becomes a new cluster. The algorithm continues until only one tree node is left. Before formally describing the algorithm, let us go through several examples. The simplest case is when there is only one data point but it is not very meaningful. Thus, let us start with two data points.
index |
x |
y |
|---|---|---|
0 |
-66 |
45 |
1 |
95 |
-84 |
They are the two children of a binary tree:
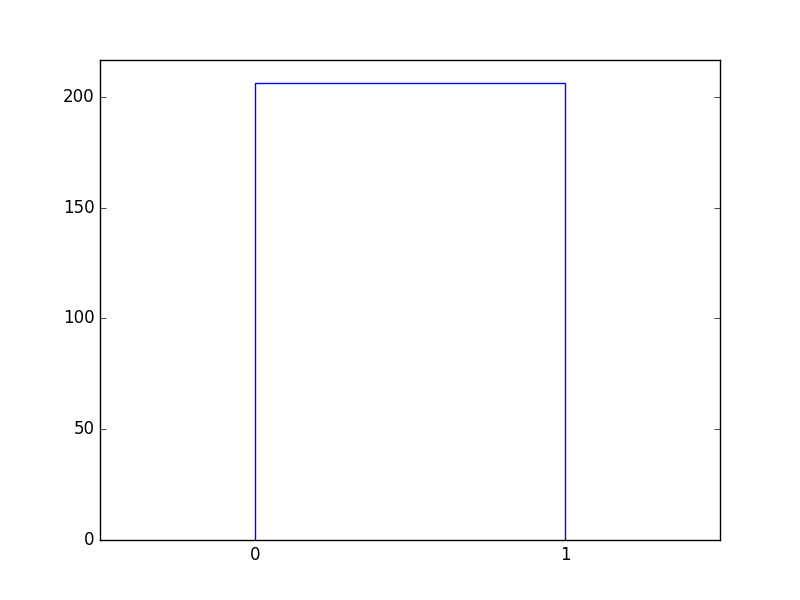
Figure 51 Two data points are the two children of a binary tree.¶
Next, we consider the case when there are four data points:
index |
x |
y |
|---|---|---|
0 |
-66 |
45 |
1 |
95 |
-84 |
2 |
-35 |
-70 |
3 |
26 |
94 |
We use the Euclidean distance here. Consider two data points: \((x_a, y_a)\) and \((x_b, y_b)\). The distance between them is defined as
\(\sqrt{(x_a - x_b)^2 + (y_a - y_b)^2}\).
Consider three data points: \((x_a, y_a)\), \((x_b, y_b)\), and \((x_c, y_c)\). The following inequality is true.
\(\sqrt{(x_a - x_b)^2 + (y_a - y_b)^2} > \sqrt{(x_a - x_c)^2 + (y_a - y_c)^2} \Leftrightarrow ((x_a - x_b)^2 + (y_a - y_b)^2) > ((x_a - x_c)^2 + (y_a - y_c)^2)\).
We care about only the order of the distance so we do not really care about the square root.
The following table shows \((x_a - x_b)^2 + (y_a - y_b)^2\) between the pairs of the data points.
0 |
1 |
2 |
3 |
|
|---|---|---|---|---|
0 |
0 |
42562 |
14186 |
10865 |
1 |
42562 |
0 |
17096 |
36445 |
2 |
14186 |
17096 |
0 |
30617 |
3 |
10865 |
36445 |
30617 |
0 |
The shortest distance (10865) occurs between \((x_0, y_0)\) and \((x_3,y_3)\). They are the first pair to be put into the same cluster. Thus, points 0 and 3 are the two children of the same parent node.
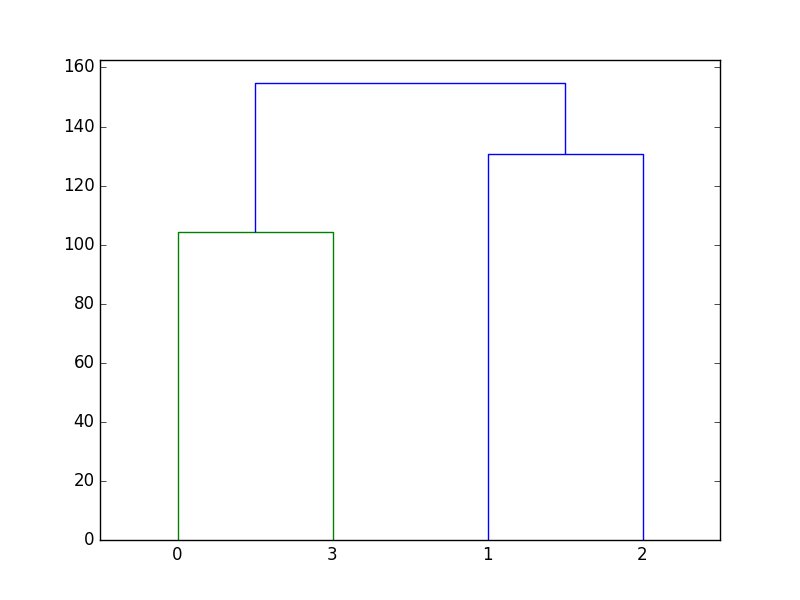
Figure 52 Clusters of four data points. Do not worry about the colors, nor the numbers along the vertical axis. Pay attention to the shape only.¶
How do we represent the cluster that includes points 0 and 3? There are several different commonly used representations. This example uses the centroid method: a cluster is represented by the centroid of the data points in the cluster. The cluster that contains \((x_0, y_0)\) and \((x_3, y_3)\) is represented by \((\frac{-66+26}{2}, \frac{45+94}{2}) = (-20, 69.5)\). This cluster is marked as the new \((x_0, y_0)\) and \((x_3, y_3)\) no longer exists. We can recompute the distances among the pairs of points:
TO DO: make the table align right
0 |
1 |
2 |
3 |
|
|---|---|---|---|---|
0 |
0 |
42562 |
14186 |
10865 |
1 |
42562 |
0 |
17096 |
36445 |
2 |
14186 |
17096 |
0 |
30617 |
3 |
10865 |
36445 |
30617 |
0 |
The shortest distance (10865) occurs between \((x_0, y_0)\) and \((x_3,y_3)\). They are the first pair to be put into the same cluster. Thus, points 0 and 3 are the two children of the same parent node.
How do we represent the cluster that includes points 0 and 3? There are several different commonly used representations. This example uses the centroid method: a cluster is represented by the centroid of the data points in the cluster. The cluster that contains \((x_0, y_0)\) and \((x_3, y_3)\) is represented by \((\frac{-66+26}{2}, \frac{45+94}{2}) = (-20, 69.5)\). This cluster is marked as the new \((x_0, y_0)\) and \((x_3, y_3)\) no longer exists. We can recompute the distances among the pairs of points:
TO DO: make the table align right
0 |
1 |
2 |
|
|---|---|---|---|
0 |
0.0 |
36787.25 |
19685.25 |
1 |
36787.25 |
0 |
17096 |
2 |
19685.25 |
17096 |
0 |
Now, the shortest distance (17096) occurs between \((x_1, y_1)\) and \((x_2, y_2)\). These two data points are the two children of a tree node. At this moment, there are only two clusters and they are the children of a binary tree node. The final result is shown below

Figure 53 Clusters of four data points. Do not worry about the colors, nor the numbers along the vertical axis. Pay attention to the shape only.¶
Next, let’s add two more data points.
index |
x |
y |
|---|---|---|
0 |
-66 |
45 |
1 |
95 |
-84 |
2 |
-35 |
-70 |
3 |
26 |
94 |
4 |
15 |
20 |
5 |
66 |
-3 |
The pair-wise distances is shown below
0 |
1 |
2 |
3 |
4 |
5 |
|
|---|---|---|---|---|---|---|
0 |
0 |
42562 |
14186 |
10865 |
7186 |
19728 |
1 |
42562 |
0 |
17096 |
36445 |
17216 |
7402 |
2 |
14186 |
17096 |
0 |
30617 |
10600 |
14690 |
3 |
10865 |
36445 |
30617 |
0 |
5597 |
11009 |
4 |
7186 |
17216 |
10600 |
5597 |
0 |
3130 |
5 |
19728 |
7402 |
14690 |
11009 |
3130 |
0 |
The shortest distance (3130) occurs between \((x_4, y_4)\) and \((x_5, y_5)\). These two data points are the two children of a node. This cluster is represented by the centroid \((\frac{15 + 66}{2}, \frac{20 + (-3)}{2}) = (\frac{81}{2}, \frac{17}{2}) = (40.5, 8.5)\). The cluster is expressed as \((x_4, y_4)\) and \((x_5, y_5)\) is removed. Now there are four data points and one cluster. The distances are shown in the following table:
0 |
1 |
2 |
3 |
4 |
|
|---|---|---|---|---|---|
0 |
0 |
42562 |
14186 |
10865 |
12674.5 |
1 |
42562 |
0 |
17096 |
36445 |
11526.5 |
2 |
14186 |
17096 |
0 |
30617 |
11862.5 |
3 |
10865 |
36445 |
30617 |
0 |
7520.5 |
4 |
12674.5 |
11526.5 |
11862.5 |
7520.5 |
0 |
The smallest distance is 7520.5 and it is between \((x_3, y_3)\) and the cluster created earlier. Thus, \((x_3, y_3)\) and the cluster are put together by making them the two childrens of a binary tree node. This process continues until there is only cluster left. The final binary tree is shown below:
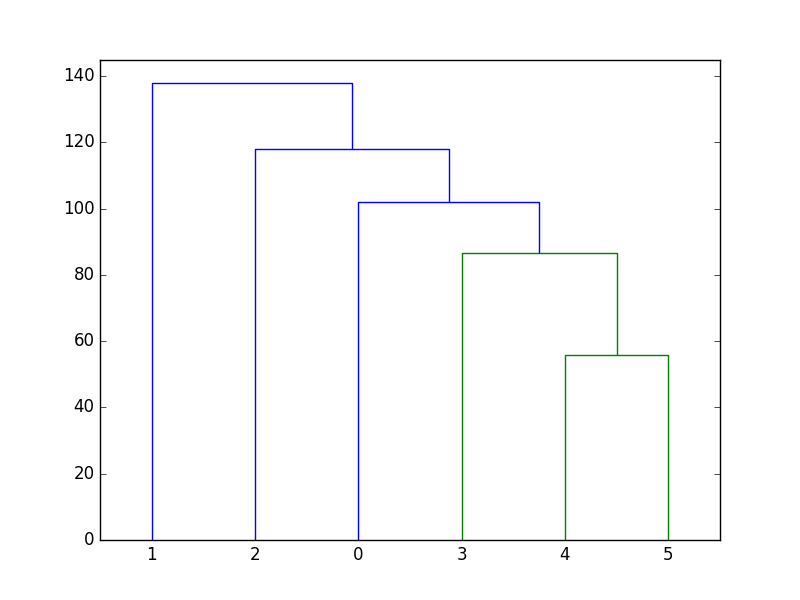
Figure 54 Cluster of the six data points.¶
The examples are generated using the following program:
#!/usr/bin/python3
from matplotlib import pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkage
import numpy as np
import random
from scipy.spatial.distance import pdist
random.seed(1)
def distance(x1, y1, x2, y2):
# no need to take square root
# print (x1 - x2, y1 - y2)
return (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2)
if __name__ == "__main__":
random.seed(1)
numdp = 6
x = []
for i in range(numdp):
x.append([random.randint(-100, 100),
random.randint(-100, 100)])
print (x)
Z = linkage(x, 'centroid')
dendrogram(Z)
plt.show()
pairdist = []
for i1 in range(numdp):
row = [0] * numdp
pairdist.append(row)
for i1 in range(numdp):
for i2 in range(numdp):
d = distance(x[i1][0], x[i1][1], x[i2][0], x[i2][1])
pairdist[i1][i2] = d
print ('pairdist', pairdist[i1])
Hierarchical Clustering Algorithm¶
The hierarchical clustering algorithm starts by treating each data point as a cluster. Then it repetively finds the closest two clusters. These two clusters are the two children of a binary tree node and form one cluster. As a result, two clusters become one cluster. This process continues until only one cluster is left. The algorithm is described below:

Figure 55 Hierarchical Clustering Algorithm¶
Define Distance of Two Clusters¶
The earlier examples use the centroid to express each cluster. Other
definitions of clusters’ distances are also used. There are four
commonly adopted definitions for the distance of two clusters (An
Introduction to Statistical Learning by James, Witten, Hastie, and
Tibshirani): complete, single, average, and centroid. They
are described below.
Suppose \(A = \{a_1, a_2, ..., a_n\}\) is a cluster and \(a_1\), \(a_2\), …, \(a_n\) are the \(n\) data points in this cluster. Suppose \(B = \{b_1, b_2, ..., b_m\}\) is another cluster and \(b_1\), \(b_2\), …, \(b_m\) are the \(m\) data points in this cluster. The distance between these two clusters can be defined as
Complete: Compute the pairwise distances of every point in \(A\) and every point in \(B\), then select the largest distance. Mathematically, the distance is defined as \(\underset{a_i \in A, b_j \in B}{\max}{|a_i - b_j|}\). Here, \(|a_i - b_j|\) means the distance of the two points.
Single. This definition considers the smallest distance among all pairs of points in \(A\) and \(B\): \(\underset{a_i \in A, b_j \in B}{\min}{|a_i - b_j|}\).
Average. This definition computes the average of the pairwise distances: \(\frac{1}{n \times m} \underset{a_i \in A, b_j \in B}{\Sigma} {|a_i - b_j|}\).
Centroid. Find the centroid \(c_A\) of \(A\) and the centroid of \(c_B\) of \(B\) using in Chapter of k-mean. The distance of the two clusters is the distance of the two centroids: \(| c_A - c_B|\).
Implementation¶
Data Structures¶
TO DO: Explain list and tree
Procedure¶
To implement hierarchical clustering, we will use two types of data structures: binary tree node and list node. Each binary tree node represents a cluster. The original data points are stored in the leaf nodes and each data point is a cluster of its own. These binary tree nodes are stored in a list. In a binary tree, a node is a leaf if it has no child. Then, the cloest two clusters are fused together into a single cluster. The two clusters are removed from the list and the new cluster is added to the list. In each step, two clusters are removed and one cluster is added. As a result, the number of clusters is reduced by one in each step. This process continues until only one cluster is left.
TO DO: Make a figure
The program’s starting point is relatively simple. It accepts one
argument as the input file. Please notice that it is different from
the k-mean solution since hierarchical clustering does not need the
value of k.
TO DO: Explain the code
#! /usr/bin/python
# main.py for hierarchical clustering
import sys
import cluster
import argparse
def checkArgs(argv = None):
parser = argparse.ArgumentParser(description='parse arguments')
parser.add_argument('-f', '--filename',
help = 'name of the data file', default = 'data.txt')
parser.add_argument('-d', '--distance',
help = 'distance definition',
choices = ('c', 's', 'a', 't'))
# four methods to measure distances between clusters:
# complete, single, average, centroid
args = parser.parse_args(argv)
return args
if __name__ == "__main__":
args = checkArgs(sys.argv[1:])
cluster.cluster(args)
# cluster.py for hierarchical clustering
import sys
from hclist import HCList
def cluster(args):
filename = args.filename
distdef = args.distance
try:
fhd = open(filename) # file handler
except:
sys.exit('open fail')
# create an empty hierarchical clustering list
hcl = HCList(distdef)
# read the data
count = 0
for oneline in fhd:
data = map(int, oneline.split())
count = count + 1
# print "add to list", data
hcl.add(data)
# print "--- finish reading file ---"
hcl.printList()
hcl.cluster()
print "--- final cluster ---"
hcl.printList()
# hctree.py for hierarchical
class TreeNode:
def __init__(self, val):
self.value = val
self.left = None
self.right = None
def printNode(self):
if (self == None):
return
if ((self.left == None) and
(self.right == None)):
print "Leaf: ", self.value
else:
print self.value
if (self.left != None):
self.left.printNode()
if (self.right != None):
self.right.printNode()
def getLeft(self):
return self.left
def getRight(self):
return self.right
def distanceComplete(self, trnd):
dist1 = self._distanceCompleteNode(trnd)
dist2 = dist1
dist3 = dist1
if (self.left != None):
dist2 = self._distanceCompleteNode(self.left, trnd)
if (self.right != None):
dist3 = self._distanceCompleteNode(self.right, trnd)
return max(dist1, dist2, dist3)
def distanceSingle(self, trnd):
return 0
def distanceAverage(self, trnd):
return 0
def distanceCentroid(self, trnd):
return 0
def _distance(self, sndnode):
sum = 0
for ind in range(len(self.value)):
dist = self.value[ind] - sndnode.value[ind]
sum = dist * dist
return sum
def _distanceCompleteNode(self, trnd):
# find the maximum distance of one node with all nodes in trnd
dist1 = self._distance(trnd)
dist2 = dist1
dist3 = dist1
if (trnd.left != None):
dist2 = self._distanceCompleteNode(self, trnd.left)
if (trnd.right != None):
dist3 = self._distanceCompleteNode(self, trnd.right)
return max(dist1, dist2, dist3)
from hctree import TreeNode
import sys
class ListNode:
def __init__(self, tn):
# double linked list, with after and before
# use after and before, not next and prev
# because next is already defined in Python
self.trnode = tn
self.after = None
self.before = None
class HCList:
def __init__(self, distdef):
# the list has a dummy node. It is both head and tail
trnd = TreeNode(None)
lsnd = ListNode(trnd)
self.head = lsnd
self.tail = lsnd
self.dist = distdef # definition of distance
# add a cluster to the list
# a new cluster is stored in a tree node
# the tree node is added to the list
def add(self, val):
trnd = TreeNode(val)
lsnd = ListNode(trnd)
self.tail.after = lsnd
lsnd.before = self.tail
self.tail = lsnd
return trnd
def delete(self, lsnd):
# cannot delete the first node (dummy)
if (lsnd == self.head):
print "ERROR, delete dummy head"
return
# delete the last node
if (lsnd == self.tail):
self.tail = self.tail.before
self.tail.after = None
return
# delete a node in the middle
before = lsnd.before
after = lsnd.after
before.after = after
after.before = before
def printList(self):
print "HCList::printList"
lsnd = self.head.after
while (lsnd != None):
lsnd.trnode.printNode()
lsnd = lsnd.after
def distance(self, lsnd1, lsnd2):
if ((self.dist == 'c') or (self.dist == 'C')):
return lsnd1.distanceComplete(lsnd2)
if ((self.dist == 's') or (self.dist == 'S')):
return lsnd1.distanceSimple(lsnd2)
if ((self.dist == 'a') or (self.dist == 'A')):
return lsnd1.distanceAverage(lsnd2)
if ((self.dist == 't') or (self.dist == 'T')):
return lsnd1.distanceCentroid(lsnd2)
print ('Unknown method for calcuating distance')
return 0
def merge(self, trnd1, trnd2):
# value not used for non-leaf nodes
val = [-1] * len(trnd1.value)
trnd = self.add (val)
trnd.left = trnd1
trnd.right = trnd2
trnd.printNode()
def cluster(self):
# this implementation is not efficient but it should
# be easy to understand
# remember that head is the dummy node
while (self.head.after != self.tail):
# at least two list nodes, not done yet
# distance of the first two list nodes as reference
lsnd1 = self.head.after
lsnd2 = lsnd1.after
mindist = self.distance(lsnd1, lsnd2)
# find the pair of the smallest distance
flsnd = self.head.after # first list node
while (flsnd != self.tail):
slsnd = flsnd.after # second list node
while (slsnd != None):
dist = self.distance(flsnd, slsnd)
if (dist < mindist): # notice, no =
dist = mindist
lsnd1 = flsnd
lsnd2 = slsnd
slsnd = slsnd.after
flsnd = flsnd.after
# remove the two nodes that have the smallest distance
# from the list
print "merge", lsnd1.trnode.value, lsnd2.trnode.value
self.delete(lsnd1)
self.delete(lsnd2)
self.merge(lsnd1.trnode, lsnd2.trnode)
return self.head.after.trnode